Découvrez pourquoi et comment l’utiliser, avec des démonstrations et des exemples concrets. (Spoiler : on parle même de plomberie, de vinyles et de freins à disque dans cet article !)
Comprendre la formule du périmètre d’un cercle
Si vous confondez aire et périmètre, vous risquez de perdre le fil rapidement ! Le périmètre, c’est ni plus ni moins que la longueur du contour d’un cercle. Pas le remplissage, pas l’intérieur, juste ce fichu fil imaginaire qui fait tout le tour. Dans la vraie vie : si vous voulez mesurer combien de ruban il faut pour entourer une assiette, c’est le périmètre qui vous sera utile.
- Contour : on parle bien du tracé qui fait tout le tour
- Longueur : résultat exprimé en cm, m… pas en cm²
- Unité : toujours une unité linéaire (jamais au carré !)
La formule officielle : P = 2πr ou P = πD, explications rapides
Deux formules ? Oui, et ce n’est pas pour t’embrouiller. En fait, c’est exactement la même chose vue sous deux angles :
- P = 2 × π × r (où r est le rayon du cercle)
- P = π × D (où D est le diamètre)
Pourquoi ce fameux facteur 2 ? Simplement car le diamètre vaut deux fois le rayon — D = 2r — alors selon ce que tu mesures en premier (rayon ou diamètre), tu adaptes ta sauce ! Le nombre π (pi) lui, c’est la constante magique qui relie diamètre et périmètre depuis la nuit des temps mathématiques. Un conseil : retiens les deux formules et utilise celle qui t’évite de sortir la calculette inutilement.
Tableau récap’ : rayon, diamètre, π — qui est qui ?
| Symbole | Définition | Unité |
|---|---|---|
| r | Rayon : distance centre → bord | cm / m |
| D | Diamètre : segment passant par le centre (D = 2r) | cm / m |
| π (pi) | Rapport entre périmètre et diamètre (~3,14159…) | sans unité |
| Périmètre | Longueur du contour du cercle | cm / m |
Attention : confondre rayon et diamètre est une erreur fréquente et peut fausser tout le calcul.
Pas à pas : comment calculer le périmètre d’un cercle sans se planter ?
Identifier rayon ou diamètre : méthodes de mesure simples (règle, compas, appli)
Pour mesurer un cercle en classe ou chez soi, voici des méthodes simples et efficaces. Trois techniques qui font le tour du sujet sans chichi :
- Avec une règle
- Pose la règle sur le cercle et repère le centre (pas au pif !)
- Mesure du centre jusqu’au bord : tu obtiens le rayon ("r")
- Pour le diamètre, mesure d’un bord à l’autre en passant par le centre
- Avec un compas
- Place la pointe sèche pile au centre du cercle
- Ouvre l’écartement jusqu’au bord ; garde cette ouverture
- Reporte la distance sur une règle : c’est ton rayon tout net !
- Avec une application mobile (type "règle AR")
- Lance l’appli et vise bien le centre du cercle à l’écran
- Balaye jusqu’au bord et valide la mesure affichée (attention aux erreurs de parallax !)
- Relève la valeur, et fais-toi respecter par les autres qui pestent contre la tech…
Anecdote amusante : deux collégiens se disputaient un smartphone pour mesurer un dessin de pizza sur leur cahier – une scène digne d’un atelier cuisine high-tech !
Choisir la bonne précision de π : 3,14 / 22/7 / touche π ?
Le nombre π (prononcé "pi") n’est ni exactement égal à 3,14 ni à 22/7 – ce sont des approximations pratiques mais imparfaites.
- 3,14 : simple mais faux dès qu’on dépasse trois décimales ; perte sèche sur les contrôles millimétrés.
- 22/7 : mieux pour du calcul mental mais reste imprécis ; chiffre historique plus qu’utile aujourd’hui.
- Touche π sur ta calculatrice : là on parle ! C’est la seule qui balance toutes les décimales dispo (souvent plus de dix).
Exemple guidé niveau 6ᵉ : du disque de 4 cm au résultat final
On balance un vrai exo comme en salle B21.
1. On te dit : « Rayon = 4 cm »
2. On utilise P = 2 × π × r, donc P = 2 × π × 4
3. Avec π ≈ 3,1416 → P = 2 × 3,1416 × 4 = 25,1328 cm
4. Arrondi raisonnable pour ton prof : 25,1 cm (si deux chiffres après la virgule demandés)
5. Dans la vraie vie : si tu coupes un fil pour entourer ce disque — vérifie bien que t’as assez à chaque millimètre près !
Vérification ultime : unités, arrondis et cohérence du résultat
Autant vous dire qu’oublier tes unités dans une réponse te vaudra direct un regard noir du correcteur.
Avant de rendre ta copie : vérifie que ton périmètre est bien exprimé dans la même unité que ton rayon ou diamètre (cm → cm, jamais cm²). Si tu trouves « cm² », c’est mort — t’as confondu avec l’aire… et ça craint.
Applications béton du périmètre d’un cercle dans la vraie vie
Le périmètre d’un cercle est une notion très concrète lorsqu’il s’agit de bricolage ou d’usinage. Derrière chaque formule se cachent des applications pratiques qui nécessitent une grande précision.
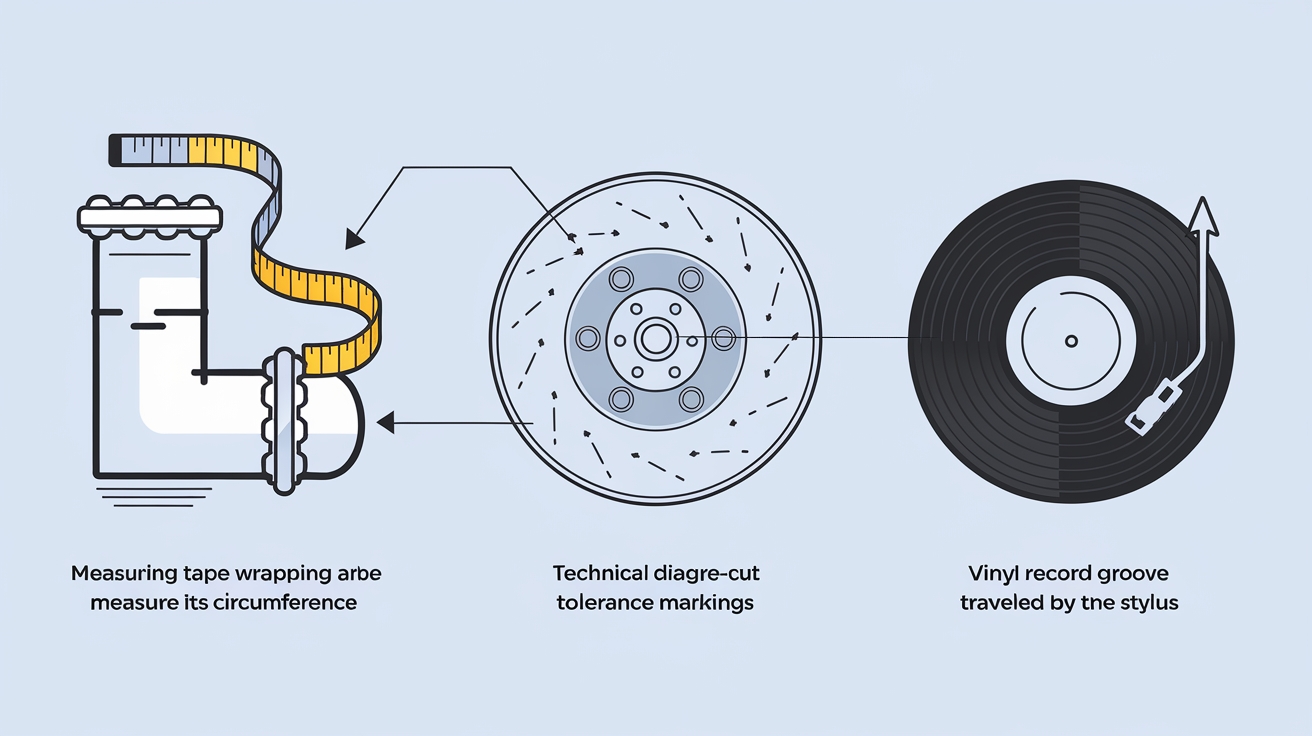
Fabriquer la bonne longueur de ruban pour cercler un tuyau (DIY plomberie)
Besoin de cercler un tube de 5 cm de diamètre, par exemple pour l’isoler avec du ruban ? On ne sort pas le mètre au pif : on applique direct la formule P = π × D. Avec D = 5 cm, ça donne P ≈ 3,1416 × 5 ≈ 15,7 cm. Tu coupes court à la galère et tu passes pour un as devant ta famille — sauf si tu oublies l’arrondi et que ça manque d’un centimètre…
Industrie : découpe laser et freins à disque
Dans l’industrie, c’est pas la fête du pifomètre. Pour tailler un disque de frein au laser (diamètre typique : 240 mm), la moindre tolérance dépassée ruine la pièce ! Une erreur d’1/10e de mm sur le périmètre se paie cash en vibration ou freinage foireux. On sort donc les outils qui claquent, calé sur π version calculatrice scientifique — ni plus ni moins.
Vinyle & audio : périmètre et durée d’écoute
Chez les diggers, rien n’est laissé au hasard. Le diamant du tourne-disque parcourt une longueur égale au périmètre multiplié par le nombre de tours (exemple : 45 tours/minute sur un disque de 10 cm de rayon → environ 62,8 cm parcourus par tour). C’est ce qui conditionne exactement combien de temps dure ta piste audio avant le silence… Les vrais savent que raccourcir le rayon réduit sec la durée écoutable.
FAQ : les questions qui reviennent tout le temps
Périmètre vs aire : pourquoi on confond encore ?
Soyons clairs : périmètre, c’est le tour du cercle, l’extérieur, la piste d’athlétisme. Aire, c’est ce qu’il y a dedans, la surface à peindre si tu veux recouvrir un disque. Si tu mélanges les deux, c’est comme confondre la longueur de ta clôture et celle de ton gazon à tondre… Erreur de débutant et zéro pointé assuré !
Circonférence, c’est quoi la nuance ?
Mini-glossaire sans bla-bla inutile :
- Cercle : figure géométrique parfaite, tous les points à égale distance du centre.
- Circonférence : ligne courbe qui fait tout le tour du cercle (le contour).
- Périmètre : longueur de cette circonférence (mesurée en cm, m…).
En vrai : "circonférence" et "périmètre" d’un cercle c’est exactement pareil côté chiffres.
Trouver le périmètre à partir de l’aire, possible ou pas ?
Oui — mais faut pas se louper dans le calcul inversé. À partir de l’aire A :
P = 2 × √(πA) (On isole r dans A = πr², puis on injecte dans P = 2πr). Le genre de formule que peu de profs osent donner en contrôle… mais ça claque pour briller en atelier math !
Convertir périmètre → diamètre → rayon : mode d’emploi rapide
Tu veux jongler entre toutes les mesures ? Voici l’algo express :
1. Tu pars du périmètre P (aussi appelé circonférence C)
2. Pour trouver le diamètre D : D = P / π
3. Pour trouver le rayon r : r = P / (2 × π)
4. Pour vérifier : P = πD ou P = 2πr
Faut juste pas zapper les parenthèses ni tronquer π comme un sauvage.
Erreurs classiques et pièges à éviter (contrôle de maths inside)
Confondre rayon et diamètre : le double qui coûte cher
Confondre rayon et diamètre est une erreur fréquente et coûteuse. On croise encore des copies où l’élève calcule P = 2πD... alors que D, c’est déjà deux fois le rayon ! Résultat ? Tu multiplies par quatre au lieu de deux. Une telle erreur t’envoie direct à –2 points minimum sur ta note. Pire : sur un cercle de 6 cm de rayon, si tu utilises le diamètre comme rayon dans la formule, tu obtiens un périmètre fictif de plus de 75 cm au lieu de 37,7 cm — ridicule et impardonnable. Je l’ai vu en contrôle, tous les ans : même topo.
Oublier les unités ou les arrondis : copier-coller de la catastrophe
Là, c’est le festival du zéro pointé. Prof demande : « Calcule le périmètre en cm ». L’élève balance « P = π × 8 = 25,12 »... mais oublie d’ajouter "cm" ou colle « cm² » comme si de rien n’était. Le correcteur ne laisse rien passer : réponse incomplète = sanction directe. Anecdote véridique : une copie où la formule était bonne mais avec "cm²" partout — résultat, moins la moitié des points !
Tronquer π comme un boucher : impact sur la note
Arrondir π à 3 ? Autant rendre feuille blanche... Sur un cercle modeste, t’es déjà hors-jeu niveau exactitude ; sur un disque industriel ou en physique appliquée, l’erreur grimpe vite à plus d’1 cm pour des rayons moyens. C’est flagrant dès qu’on pousse le calcul : même pour un disque courant (diamètre 10 cm), utiliser π = 3 au lieu de 3,14 fait chuter ton périmètre à 30 cm contre 31,4 cm attendus !
Outils malins pour aller plus loin
Autant vous dire : marre de galérer au moindre exercice sur les cercles ? Voici le kit d’outils qui te fera passer pour un tueur à la prochaine interro – et pas juste devant l’écran !
Calculatrice scientifique : touche π, mode radian et zéro approximation
Sur ta Casio FX92 ou Texas Instruments collégien, la touche π planque souvent en haut à gauche ou en jaune (appuie sur [SHIFT] ou [2nde] puis sur la touche avec π). Cette touche balance direct 3,141592653… Pas de triche ni arrondi foireux !
- Pour taper "P = 2 × π × r", tu saisis simplement :
2,×,π,×, ton rayon, puis=, basta. - Le mode radian ? Pour les angles uniquement – ne te fais pas avoir, ça n’a rien à voir avec le périmètre.
- Conseil : vérifie que ta calculatrice est en mode "DEG" (degrés), sinon les réponses risquent d’être à côté de la plaque sur certains exos…
Convertisseurs en ligne & applis mobiles : gain de temps assuré
Fini le casse-tête, y’a des sites comme calculis.net ou Omni Calculator qui transforment ton rayon ou diamètre en périmètre instantanément. Tu rentres une valeur, ça calcule tout seul – même pour convertir circonférence ↔ rayon ↔ diamètre. Pratique quand le cerveau sature après deux exercices !
Exercices interactifs pour s’entraîner : plateformes qui claquent
Trois adresses béton pour muscler tes réflexes :
- linstit.com : exos interactifs sur la géométrie du cercle (vocabulaire, tracé, manipulations).
- Maths à la maison : exercices ciblés collège avec correction immédiate.
- MOOC conseillé : France Université Numérique (FUN) propose parfois des modules spécial maths niveau collège/lycée — inscription gratos mais faut se bouger pour suivre.
✔️ 3 actions concrètes pour progresser vite :
- S’entraîner chaque semaine avec des quiz corrigés (exemple : linstit.com)
- Utiliser systématiquement la touche π plutôt que 3,14 sur les calculs difficiles
- Croiser ses résultats avec un convertisseur en ligne (double vérif = zéro boulette)
Vous voilà armé pour dompter n’importe quel cercle
Désormais, rayon, diamètre et π ne devraient plus vous poser de problème. Dans la vraie vie, connaître la différence (et appliquer la bonne formule) fait de vous quelqu’un de précis, efficace et franchement respecté — que ce soit pour mesurer un tuyau, calculer la longueur d’une piste audio ou réussir vos contrôles. Bref : stop aux approximations, place à la confiance mathématique !
À vous de jouer : notez cet article (1 à 5 ⭐ avec emoji en commentaire — c’est le moment de donner votre verdict !)