La méthode qui change la vie des élèves (même ceux qui détestent les maths). Ce texte fleuve est le plus important qu’on ait publié. On vous explique pourquoi.
Comprendre la conjecture en mathématiques : définition et enjeux
Autant vous dire, si vous confondez encore Conjecture, Mathématiques et Théorème, c’est que le système éducatif vous a grugé. Soyons clairs : la conjecture, c’est l’oxygène de la pensée mathématique. Loin de la statue figée du Théorème ou du dogme sec d’un Axiome, la conjecture c’est le pari risqué posé sur l’autel du doute collectif. Dans la vraie vie des maths – pas dans les manuels aseptisés – une conjecture surgit quand un motif semble trop régulier pour être un hasard mais trop retors pour être avalé tout cru.
- Conjecture : Énoncé admis comme probablement vrai à force de motifs observés, mais zéro preuve béton au compteur.
- Hypothèse : Supposition de départ, souvent temporaire, qu’on balance pour tester un raisonnement.
- Théorème : Énoncé démontré à partir d’axiomes (on n’y touche plus).
- Axiome/Postulat : Vérité fixée arbitrairement comme point de départ — pas le droit d’y toucher sous peine de tout faire exploser.
Exiger une preuve dès qu’on gratte un motif ? Absurde. La conjecture, c’est la prise de risque intelligente adoptée par n’importe quel cerveau affûté. Les grandes avancées ne partent jamais d’un théorème sorti du chapeau ; elles émergent parce qu’un matheux a flairé le filon sans pouvoir l’exhiber tout de suite devant le tribunal des axiomes.
La conjecture : un point de départ pour les grandes découvertes
Dans la vraie vie – je parle pour ceux qui traînent dans les antichambres des labos ou qui bidouillent sur leur calculette jusqu’à trois heures du mat’ – aucune trouvaille majeure ne débarque déjà ficelée en démonstration. La recherche fondamentale, c’est du terrain vague où on devine plus qu’on ne sait. Prenez Gauss avec sa fameuse conjecture sur la répartition des nombres premiers : il balançait ses intuitions avant même que les outils nécessaires à leur validation n’existent ! Pareil pour le nombre de Skewes – truc complètement délirant anticipé bien avant qu’on ait les moyens informatiques pour le confirmer.
« Le raisonnement commence là où le dogme s’arrête. » – Réapproprié par Germain
Pourquoi la conjecture précède (presque) tout résultat majeur
La tension, c’est simple, elle est là : le cerveau capte des motifs avant que la logique ait chaussé ses lunettes. Pour un matheux, flairer une conjecture, c’est pas du flou artistique – c’est du radar affûté ! Yvan Monka l’a vécu cash : en classe, il repère par hasard une régularité entre des puissances de deux et des chiffres binaires. Il gratte, questionne ses élèves, ça se transforme en mini-théorème local… qui plus tard s’avère être un lemme connu dans la littérature. Moralité ? Les vrais coups de génie partent rarement d’une formalisation froide ; l’intuition bouscule, puis seulement la rigueur embarque.
« Soyons clairs : l’intuition n’est pas un péché, c’est un starter. »
L’écart clé entre conjecture, hypothèse et théorème
Soyons clairs, confondre tout ce joli monde — c’est s’interdire de piger comment la machine mathématique carbure. Le formalisme, c’est plus qu’un vernis : chaque terme impose ses propres règles du jeu. La conjecture, c’est la conviction sans preuve ; l’hypothèse, le caillou jeté pour avancer ; le théorème, l’armure certifiée de la raison. Et le postulat ? On l’avale sans broncher, sinon tout s’écroule !
- Le contre-exemple, c’est la dynamite du matheux : il pulvérise conjectures et hypothèses sans pitié – mais il ne touche JAMAIS ni axiome ni théorème !
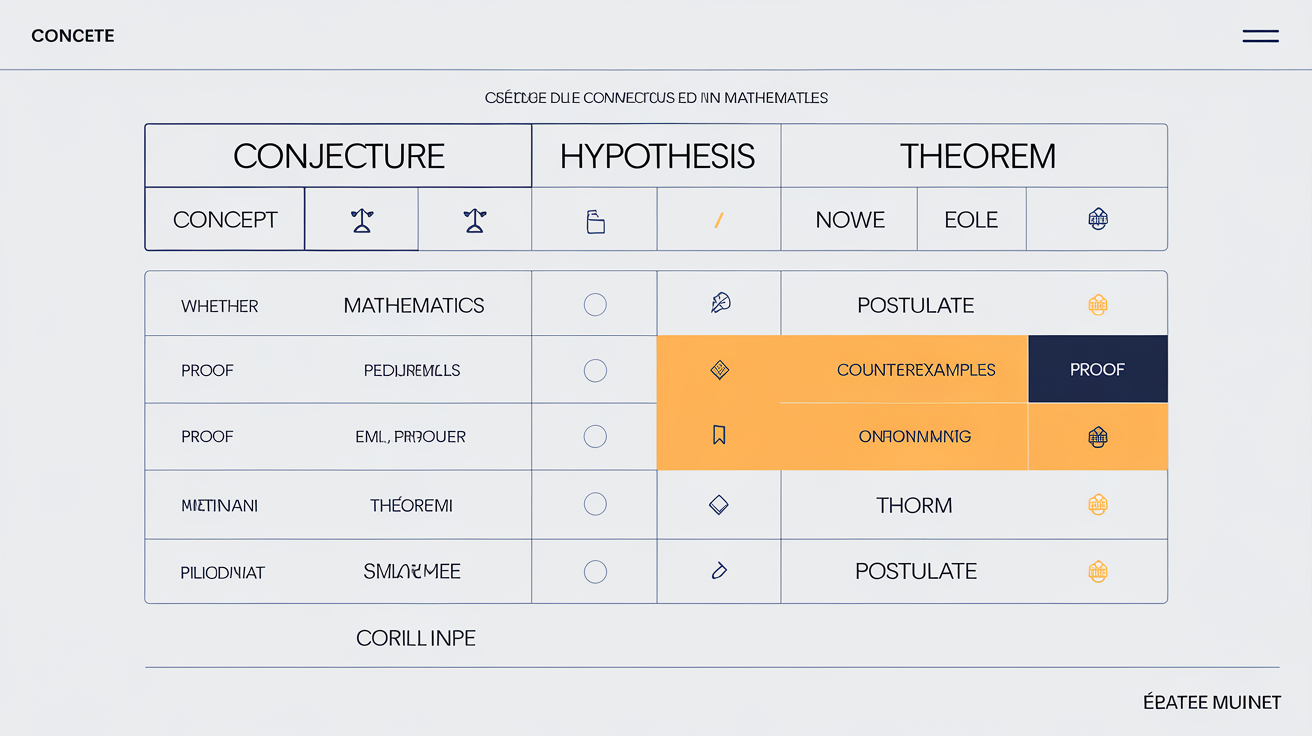
| Terme | Définition | Exigence de preuve | Exemples iconiques |
|---|---|---|---|
| Conjecture | Affirmation considérée plausible à partir d’observations mais non démontrée | Pas requise | Goldbach, Syracuse |
| Hypothèse | Supposition posée pour argumenter ou explorer | Parfois requise | Hypothèse de Riemann (avant preuve) |
| Théorème | Proposition démontrée rigoureusement | Preuve obligatoire | Pythagore, Fermat (dernier) |
| Postulat | Principe admis sans démonstration comme base | Jamais exigée | Postulats d’Euclide |
Résumé flash : seul le contre-exemple fait tomber conjectures et hypothèses; un théorème tient bon quoiqu’il arrive.
Formuler une conjecture pas à pas : méthode express sans blabla
Autant vous dire, tous ceux qui pensent que la conjecture se fabrique en méditant sur un caillou ou en recopiant le prof dans un coin de la feuille n’ont rien capté à la cuisine mathématique. Soyons clairs : il y a une recette, souvent trash mais hyper efficace. Et elle démarre par l’œil, pas par le dogme.
Observation empirique : capter les motifs récurrents
Avant de jouer les devins, faut sortir GeoGebra ou Python et traquer du motif comme un hacker en manque de patterns. Tu balances des suites de rectangles sur GeoGebra, tu observes comment ils poussent—bim, tu repères une croissance régulière ou un retour cyclique qui pue la structure cachée. Prenons deux entités emblématiques :
- Rectangle : Tu varies la longueur, tu regardes comment l’aire réagit… Surprise ! Un motif linéaire ou quadratique apparaît ?
- Triangle : Tu joues sur la base et la hauteur, et d’un coup tu vois que l’aire grimpe toujours d’une certaine façon. Bingo !
Résumé cash : c’est en triturant des objets concrets avec des outils comme GeoGebra qu’on renifle les régularités sous-jacentes — pas devant un tableau noir figé.
Généralisation prudente : écrire l’énoncé minimaliste
Maintenant, on passe du cas particulier au général – mais mollo ! La tentation du grandiloquent doit rester au vestiaire. Un énoncé minimaliste en langage matheux ressemble à ça :
- « Pour tout entier naturel n ≥ 2, le rectangle construit selon la règle f(n)… vérifie P(n). »
Ou pour les triangles ?
- « Tout triangle dont les côtés respectent [condition], possède [propriété]. »
Avant publication, trois cases à cocher SANS TRICHER :
- [ ] Variables bien définies (tu sais ce que chaque lettre fout là ?)
- [ ] Conditions initiales explicites (exit le flou artistique)
- [ ] Universalité testée sur plusieurs cas (sinon c’est de la poudre aux yeux)
Test rapide : chercher le contre-exemple assassin
Le moment bourrin arrive : tu codes un mini-script Python pour dégainer les cas tordus. Parade acrobatique inutile sans cela ! Tape dans ta conjecture jusqu’à ce qu’elle craque — la chasse au bug façon brute épaisse. Hypothèse de Riemann ? Personne n’a trouvé de contre-exemple… mais chaque script lancé est une bastos tirée sur le mythe.
Dans la vraie vie, un seul contre-exemple flingue le château de cartes — et ça personne ne te le dira à l’examen…
Conjectures célèbres qui font transpirer les matheux (et pourquoi elles comptent)
Qui a décrété qu’en maths, il fallait chercher la paix de l’esprit ? Certainement pas les monstres sacrés qu’on s’apprête à croiser ci-dessous. Chaque conjecture majeure est un champ de mines intellectuelles où même le plus froid des cerveaux transpire à gouttes larges. Place à trois légendes, chacune son délire, son terrain piégé !
Hypothèse de Riemann : la diva de la théorie des nombres
Autant vous dire, celle-ci c’est le boss final du jeu. L’hypothèse de Riemann gravite autour d’une fonction d’apparence inoffensive : la fameuse ζ(s), prononce « zêta » pour briller en soirée. Formellement :
$$
\zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s}
$$
Mais le feu commence vraiment quand on s’intéresse à ses zéros non triviaux : ces mystérieux points où la fonction s’annule sur le plan complexe. Riemann balance que tous ces zéros sont alignés pile poil sur la droite Re(s)=1/2… énorme si vrai, car cela contrôlerait au millimètre l’imprévisibilité des nombres premiers. Sauf que personne n’a réussi à prouver ce bazar depuis 1859 !!
« On connaît des milliards de zéros sur cette fameuse droite… mais zéro preuve générale. La suspicion est totale. »
Conjecture de Syracuse : la boucle infernale en 3n+1
Tu prends n’importe quel entier positif (genre ton âge, ou le nombre de tickets resto claqués ce mois-ci), tu appliques à répétition deux règles débiles : pair ? Tu divises par deux ; impair ? Tu fais 3×n+1. Le tout converge TOUJOURS vers ce cycle absurde : 4 → 2 → 1… enfin, c’est ce que tous les tests informatiques hurlent depuis des décennies — mais aucune preuve universelle !
Anecdote véridique : un prof a grillé sa soirée à faire tourner un script Python jusqu’à n = 10^16 sans jamais tomber sur une exception. Statistiquement insoluble, mathématiquement rageant.
🔥🔥🔥 frustration
Hypothèse du continu et l’ombre de Gödel : bienvenue dans l’indécidable
Là on quitte les jeux d’enfant pour se frotter au vertige : existe-t-il un infini « intermédiaire » entre celui des entiers et celui du continu (réels) ? Cantor a posé la question, baptisée hypothèse du continu. Problème : Gödel et Cohen ont prouvé qu’on ne pourra JAMAIS décider si c’est vrai ou faux via les axiomes standard de la théorie des ensembles — indécidabilité totale.
Le rêve d’un classement parfait des infinis ? Enterré par la logique elle-même. Autant vous dire : c’est pas demain qu’on boucle l’affaire.
L'indécidable : ces casse-têtes sans solution
Théorème d’incomplétude : terrain miné pour les esprits cartésiens
Autant vous dire, la promesse d’un système mathématique sans faille est un mirage pour stagiaire. Kurt Gödel a fracassé le rêve cartésien en 1931 : dans TOUT système axiomatique assez costaud pour contenir l’arithmétique basique (intégrez bien l’addition et la multiplication), il existe des énoncés indécidables — impossible à prouver, impossible à réfuter. Le premier choc, c’est que même avec la rigueur la plus froide, t’auras toujours des trous noirs logiques qui te font un doigt d’honneur.
Mais attention, Gödel n’est pas tout seul sur le ring. Youri Matiiassevitch débarque plus tard et clôt avec brio le problème de Hilbert sur la décidabilité : il montre qu’il existe des équations diophantiennes sans algorithme universel pour décider si elles ont une solution ou non. Autrement dit : même avec toute l’informatique du monde, certains problèmes resteront orphelins de preuve. Moralité ? L’indécidable n’est pas une impasse, c’est un saut dans l’inconfort créatif – bienvenue dans le vrai sport cérébral !
Dans la vraie vie mathématique, croire que tout s’explique revient à jouer au poker sans bluff : tu perds à tous les coups.
Cardinalité et ensembles infinis : la frontière floue des possibles
Soyons clairs : jouer avec l’infini, ce n’est pas les montagnes russes du parc du coin. Pour piger la différence entre dénombrable et continu, rien ne vaut l’hôtel de Hilbert (le Infinity Hotel). Imagine un hôtel avec une infinité de chambres numérotées 1,2,3… Toutes occupées ! Pourtant tu peux encore loger un nouveau client en décalant chacun d’une chambre – magouille typique de l’ensemble dénombrable (genre N).
Mais quand arrivent les réels (ensemble continu), fini la combine : impossible d’établir une bijection entre N et R. Leur cardinalité explose – on passe à une infinité qualitativement supérieure, notée $𝔠$ (cardinal du continu). Et là, question fatale : existe-t-il une taille d’infini entre ces deux mondes ? C’est l’hypothèse du continu… indécidable dans ZFC (la théorie standard des ensembles). Résultat ? On reste sur le fil du rasoir pédagogique : enseigner ces limites donne envie de creuser — pas juste bachoter.
Résumé cash : L’indécidable met le feu sous la paillasse de l’apprentissage mathématique — c’est là qu’on arrête enfin d’avaler des théorèmes prémâchés.
Conjecturer en classe : guide pratique pour profs et étudiants
Soyons clairs : la conjecture, c’est pas une lubie d’élite, c’est la base pour muscler le cerveau à tous les étages du système scolaire. Marre des exercices prémâchés ! Place à la bidouille et au test direct, même avec des mômes de collège ou des taupins surentraînés.
Activités clé-en-main du collège à la prépa
- Géométrie dynamique (Cube)
- Sur GeoGebra, faites manipuler un cube : demandez aux élèves d’explorer les différentes diagonales. L’objectif ? Leur faire émettre une conjecture sur le nombre de segments reliant deux sommets non adjacents. Qu’ils valident leurs hypothèses en tournant le cube dans tous les sens – erreur obligatoire pour piger !
- Suites numériques (Pyramide)
- Proposez une pyramide numérique où chaque étage obéit à une règle. Demandez la somme des éléments de l’étage n, puis faites conjecturer sur une formule générale. Comparez conjecture et réalité sur Maple ou Python.
- Graphes (Cycle fermé)
- Donnez un graphe représentant les coins d’une pyramide et reliez-les façon « labyrinthe ». But du jeu : combien de cycles fermés peut-on tracer sans repasser par la même arête ? Les élèves posent leur propre conjecture… et se prennent les pieds dans leurs contres-exemples.
Résumé cash : la conjecture s’attrape par manipulation, pas par récitation !
Évaluer sans tuer le doute : barème centré sur démarche
Pas de note-sanction façon bûcher. Ce qui compte, c’est la trajectoire intellectuelle, pas juste le résultat final. Barème recadré :
| Critère | Points | Commentaires |
|---|---|---|
| Observation pertinente | 4 | Motifs bien captés |
| Tentative de généralisation | 5 | Énoncé clair, variables définies |
| Test(s) critique(s) / Recherche de contre-exemple | 6 | Démarche explicite |
| Révision ou ajustement après essai | 3 | Capacité d’auto-correction |
| Justification orale/écrite | 2 | Clarté de l’explication |
Total : 20 points – t’as compris ou tu bluffes ?
Outils numériques (GeoGebra, Python)
Arrêtez avec les paperboards poussiéreux ! Les vrais outils pour tester ses hypothèses en mode turbo :
- GeoGebra – Pour manipuler figures et objets dynamiquement (exemples avancés sur GeoGebra)
- PyGgb – Intégrez Python direct dans GeoGebra… Visualisation + code en simultané (PyGgb sur GitHub)
- Notebooks Jupyter – Idéal pour investiguer des suites ou générer des contre-exemples massifs.
- Maple/Mathematica – Pour ceux qui veulent automatiser tests et visualisations balèzes.
Autant vous dire : si tu n’as jamais fait bugger GeoGebra avec une conjecture foireuse, t’as raté ta jeunesse mathématique.
Les erreurs classiques quand on veut « prouver » trop vite
On va pas se mentir, la « preuve » à l’arrache, c’est le virus mortel de tous les clubs de maths du lundi soir. Deux pièges majeurs qui t’envoient direct en zone rouge :
Confondre corrélation visuelle et preuve formelle
Autant vous dire : dessiner trois jolis carrés et choper une règle apparente, ça fait joli en story Insta mais c’est pas un argument ! Un carré, c’est un rectangle particulier — mais la réciproque ? Zéro garanti par le dessin. Les contre-exemples pullulent dès qu’on bricole un peu : certains rectangles ne seront jamais des carrés, même si la figure est bien léchée au tableau.
Dans la vraie vie mathématique, une intuition graphique doit se faire allumer à coups de contre-exemples ou de preuves rigoureuses. Sinon tu fonces droit dans le mur — cf. tous les débats foireux sur Reddit où la "preuve visuelle" finit carbonisée.
Ignorer les conditions initiales : le piège fatal
Soyons clairs : oublier de fixer correctement les bornes, le domaine ou les variables ruine toute tentative de démonstration. Le cas Skewes est croustillant — ce nombre monstreux montre que certaines régularités (la fameuse distribution des nombres premiers) semblent tenir... jusqu’à ce que tu atteignes une borne où tout s’effondre !
Avant même de taper ta première ligne de preuve, checke cette liste (sinon t’es mort) :
- Domaine d’application bien défini ?
- Bornes explicites et justifiées ?
- Variables toutes déclarées ?
- Exemples testés dans la zone critique (pas juste sur 1, 2 ou 3...)
Résumé : Ceux qui négligent ces checks vivent dans l’illusion mathématique pendant que leur conjecture coule au premier vrai test.
FAQ : tout savoir sur les conjectures
Une conjecture peut-elle devenir fausse ?
Soyons clairs : une conjecture n’est pas un dogme, c’est un pari. Et parfois, ce pari se plante méchamment ! Prenez l’exemple de la conjecture de Pólya (1958) sur les coefficients des fonctions entières à valeurs réelles : tout le monde y croyait dur comme fer… jusqu’au jour où Haselgrove balance un contre-exemple assassin qui la pulvérise pour de bon. Même topo côté nombres premiers : la fameuse conjecture de Legendre ("il existe toujours un nombre premier entre deux carrés consécutifs") tient encore debout — mais d’autres, comme celle de Ganea ou Hauptvermutung, sont tombées sous les coups des exemples tordus. Moralité ? Faut jamais graver une conjecture dans le marbre tant qu’un contre-exemple malin peut traîner dans le coin.
Qui décide qu’une preuve est valide ?
Dans la vraie vie, c’est pas le prof du fond ni une IA qui valide une preuve balèze, mais toute une armée d’humains plus ou moins obsessionnels. Le circuit ? Un mathématicien pond la démonstration et balance ça dans une revue sérieuse ou direct sur arXiv pour décapitage public en mode open-source. Le peer-review, c’est la chasse aux failles : plusieurs matheux indépendants fouillent chaque ligne à la recherche du bug fatal avant acceptation officielle. Sauf que même là, il y a raté de temps en temps — voir les bourdes dans les archives historiques ! Pour les débats plus pointus ou rapides, place nette à MathOverflow où tout le monde peut scruter et critiquer une "preuve" en live.
Mon avis — Germain Drouet sort le fusil :
Franchement, dépendre du cénacle fermé des revues pour valider la vérité mathématique ? Zéro vision ! Je plaide pour un modèle open-source massif : tous les scripts, toutes les preuves dispo publiquement, examinées par des passionnés ET des pros. C’est comme ça qu’on évite les dogmes poussiéreux et qu’on fait avancer vraiment le schmilblick collectif.
Pourquoi le doute est essentiel en mathématiques
Je persiste à penser que la méthode – flairer, généraliser, cogner sur les contre-exemples – n’est pas réservée aux pontes ; tout élève qui ose douter progresse cent fois plus vite. L’indécidable, loin d’être une impasse, m’oblige à sortir du rail et bouscule ma routine didactique : c’est là que l’innovation jaillit. Enfin, la beauté du doute – ce sentiment de marche sur des œufs mathématiques – vaut toutes les certitudes prémâchées du programme.
« Le doute n’est pas une faille ; c’est le carburant de la découverte. » – GD
Soyons clairs : on n’a pas fini de pousser les murs de l’inconnu.






