Dans une classe de 4ᵉ, il est courant de trouver 3 catégories d’élèves :
1) Ceux qui adorent le calcul littéral car ils y voient enfin une utilité concrète aux maths ;
2) Ceux qui le détestent car ils le trouvent trop abstrait et incompréhensible ;
3) Ceux qui n’ont pas encore compris qu’ils font partie de la 2ᵉ catégorie.
Et pour cause : s’il y a bien une notion qui fait consensus sur son importance, c’est celle-ci.
Autant chez les enseignants que chez les élèves.
Pourquoi ? Car le calcul littéral est un outil d’une puissance inouïe pour modéliser des situations ultra-concrètes.
Le problème ? C’est aussi l’une des notions les plus exigeantes du programme.
Résultat : chaque année, des centaines de milliers d’élèves se retrouvent en difficulté.
Et s’exposent à des lacunes qui leur coûteront très cher les années suivantes.
Sauf qu’on est bien décidés à ne pas laisser faire.
Alors, on vous a préparé le cours ultra-complet sur le calcul littéral en 4ᵉ.
Avec :
→ Le cours complet : méthodes, propriétés et formules incontournables
→ 20 exercices avec corrigés détaillés
→ Les erreurs à éviter et astuces pour les surmonter
→ Fiches mémo PDF à télécharger gratuitement.
À lire ici https://lnkd.in/e4tN8Yc6
PS. Pensez à partager à un parent/élève/prof qui en aura l’usage .
Calcul littéral 4ᵉ : la définition qui met tout le monde d’accord (sans bla-bla)
Si tu crois que le calcul littéral en 4ᵉ se résume à coller des chiffres à la place des lettres, détrompe-toi ! On aborde ici une notion clé du programme, essentielle pour poser des situations générales avec rigueur. Le calcul littéral, c’est LA clé pour poser des situations générales avec rigueur — pas juste bidouiller un x ou un y pour faire joli.
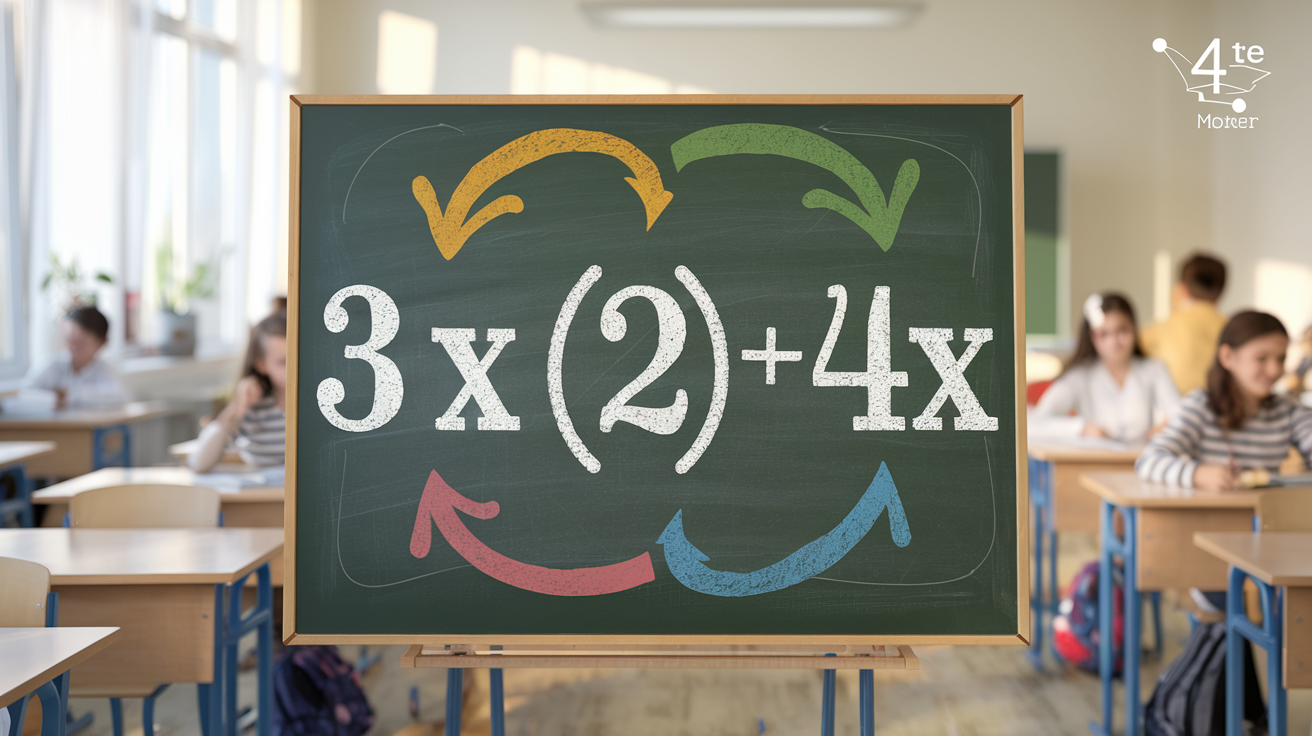
« Remplacer x par 7 ne résout pas tout : c’est comme croire qu’une clé anglaise suffit pour démonter une fusée. »
Dans ce bazar organisé, la variable (x) te sert à modéliser tout ce qui peut changer (nombre d’élèves, taille d’un escalier IKEA), la constante reste figée (prix fixe, hauteur d’une marche), et le coefficient ? C’est l’amplificateur discret du problème.
Pourquoi on mélange chiffres et lettres : l’utilité réelle en math et dans la vraie vie
Dans la vie quotidienne, le calcul littéral est un outil pratique et omniprésent :
- Recette adaptable : Pour n crêpes, quantité de lait = 50 × n (et si t’as déjà foiré un brunch parce que t’as mal multiplié, tu piges l’intérêt…)
- Programmation/algorithme : La boucle qui dit « pour chaque joueur x : score_total = score_total + points(x) »
- Montage IKEA : Nombre de planches à acheter = 2 × étagères + portes – vis perdues (et oui, ça sent le vécu)
Les 3 notions cœur du programme (expression, variable, égalité) en 120 s chrono
- Expression littérale : Un assemblage savant de chiffres et de lettres. C’est ton plan d’action avant même d’avoir les infos complètes.
- Variable : L’inconnue qui change la donne à chaque situation – ni sorcière ni devinette.
- Égalité : Ce qui garantit que ta manip’ tient debout mathématiquement (« ce que tu fais à gauche, faut pouvoir le refaire à droite sans créer un bug cosmique »).
Formules et propriétés incontournables du calcul littéral niveau 4ᵉ
Si tu as manqué la distributivité en cours, tu risques de rencontrer des difficultés dès qu’il s’agit de simplifier des factures ou de coder des lignes valables. Les manuels se gavent à saupoudrer la règle sans jamais te montrer le vrai piège : « appliquer bêtement » sans piger le sens = aller droit dans le mur. Allez, on pose les bases – et que ça saute !
Développer : distributivité simple & double (CH2, CH3)
- Distributivité simple : a × (b + c) = a × b + a × c. (Par exemple : 2(x + 4) = 2x + 8)
- Distributivité double : (a + b)(c + d) = a(c + d) + b(c + d) → puis tu développes chaque terme ! Exemple célèbre : (x + 1)(x + 3) = x(x+3) + 1(x+3) = x² + 3x + x + 3.
| Type | Forme | Exemple | Piège classique |
|---|---|---|---|
| Simple | a(b+c) | 5(x+2) = 5x + 10 | Oublier de distribuer à tous les termes |
| Double | (a+b)(c+d) | (y+4)(y-2) = y²+2y-8 | Croire qu’on distribue juste au premier terme et zapper la suite ! |
Facture de pizzas ? Si chaque pizza coûte (6 € + supplément à x €), alors pour n potes affamés ça donne n(6+x). Si tu rates la distributivité, tu paies double — c’est du vécu…
Réduire : regrouper les termes semblables comme un pro
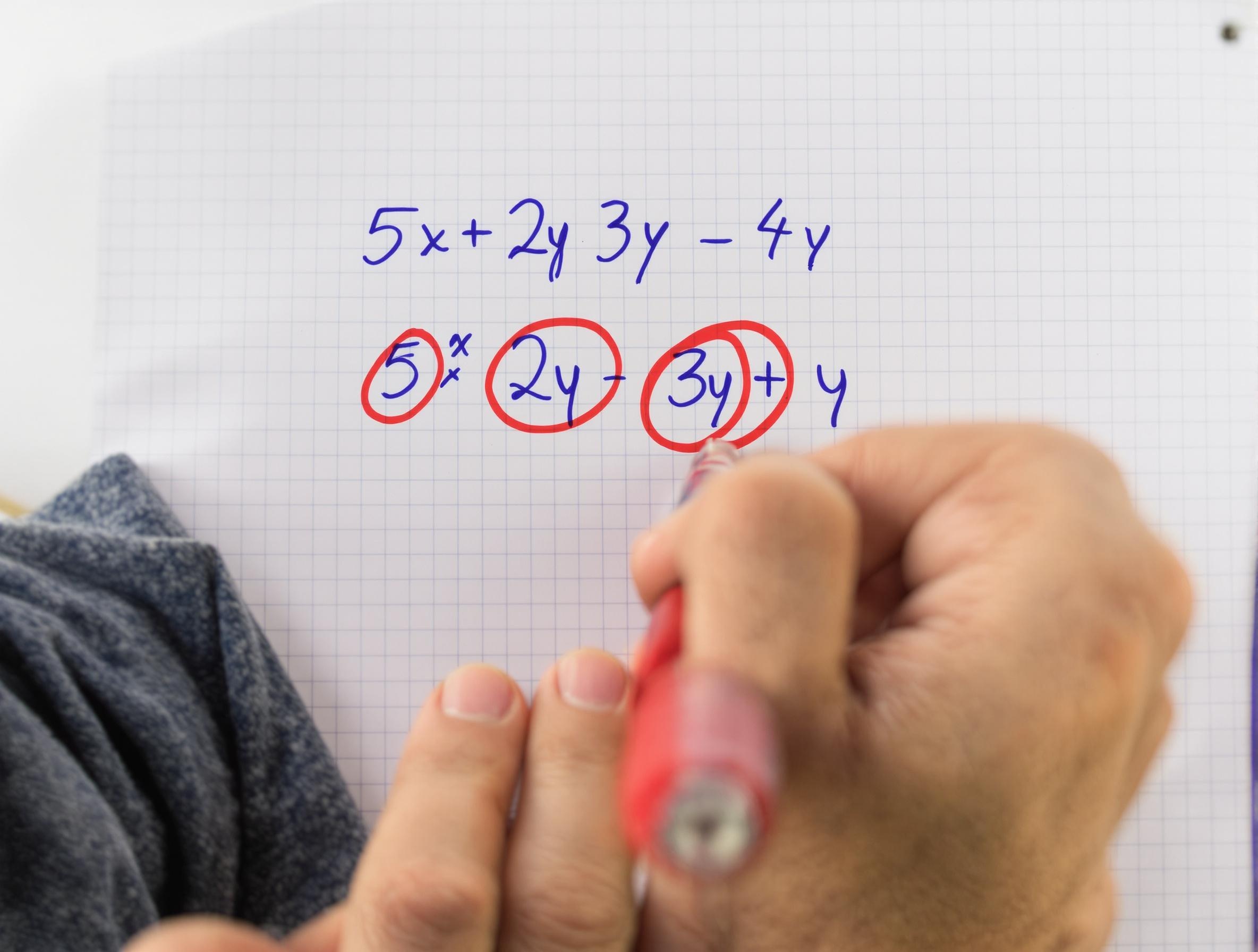
Le tri des termes, c’est comme séparer le linge sale avant de lancer la machine : tu mélanges pas les chaussettes rouges avec tes t-shirts blancs. Regroupe les mêmes variables puis additionne/soustrais leurs coefficients. Exemple limpide :
5x + 2y – 3x + y devient (5x – 3x) + (2y + y) = 2x + 3y.
Attention aux signes devant chaque terme : -x n’est pas ton ami si tu lis trop vite !
Factoriser : l’art de remonter la pelote (mise en évidence, CH4)
Factoriser, c’est retourner l’opération de développement. Tu repères le facteur commun comme un détective grille-pain — et tu mets en évidence pour condenser l’expression.
Exemple CH4 classique :
4a + 8b = 4(a+2b).
C’est littéralement faire l’opération inverse du développement, mais faut avoir l’œil pour ne pas louper ce qui est commun…
Méthode pas-à-pas pour résoudre une expression littérale sans planter (workflow gagnant)
Tu veux pas finir dans le décor ? Voici la méthode qui évite les bourdes typiques.
Étape 1 – Identifier le type d’opération : somme, produit, puissance
Soyons clairs : avant de tout mélanger, repère ce que tu as sous les yeux. Scénario express : on te donne l’expression 3(x + 2)² + x. Est-ce une somme ? Un produit ? Une puissance ? Pose-toi franchement ces questions :
- Y a-t-il un + ou un – ? → Somme/Différence
- Un signe × collé à une parenthèse ou deux lettres côte à côte (ex : 4x) ? → Produit
- Un exposant (², ³…) ? → Puissance
- Plusieurs types qui se mélangent ? → Mets en surbrillance chaque partie !
Checklist rapide :
- [ ] J’ai coché si c’est une somme/différence
- [ ] J’ai repéré les produits
- [ ] J’ai noté s’il y a des puissances
Étape 2 – Appliquer la bonne propriété (check-list visuelle)
À chaque type son arme fatale. Les vrais champions n’oublient jamais CH5 :
- Somme/Différence ? ➡️ Regroupe termes semblables (2x + 5x = 7x)
- Produit ? ➡️ Distributivité (a(b + c) = ab + ac)
- Puissance ? ➡️ Rappelle-toi : (a^m) × (a^n) = a^(m+n)
- Parenthèses partout ? ➡️ Développe puis réduis avant toute autre manip’
Étape 3 – Vérifier la cohérence numérique : astuces d’auto-contrôle
Le move ultime du survivant des heures de colle : chope un x simple comme x=1. Tu remplaces partout et tu calcules d’abord avec l’expression initiale, puis avec ta version simplifiée.
Si t’obtiens pas le même résultat, t’as loupé un épisode.
Exemple vécu :
Si tu simplifies 2(x+3)+4x en pensant que ça fait 2x+3+4x, tu prends x=1 → à gauche : 2(1+3)+4×1 = 8+4=12 ; à droite : 2×1+3+4×1=2+3+4=9. Oups, carton rouge !
Top 7 des erreurs de calcul littéral en 4ᵉ (et comment les éviter)
Erreur n°1 : Confondre addition et multiplication (l’oubli fatal du ×)
Classique : écrire 3x + 2x = 5x puis croire que x+x=2x suffit à tout expliquer. Mauvais réflexe ! Si tu zappes le ×, exemple : 4(2 + x) ≠ 8 + x.
Correctif : Toujours distribuer le chiffre devant la parenthèse à chaque terme.
Erreur n°2 : Disséquer une distributivité mal appliquée
Tu te crois rapide et tu fais : 2(x + 5) = 2x + 5 (tu as oublié de multiplier le 5). Autant dire que c’est carton rouge immédiat.
Correctif : À chaque terme sous la parenthèse, applique la multiplication. Ici : 2(x+5)=2x+10.
Erreur n°3 : Variables mal alignées (quand x² n’est pas 2x)
Piège récurrent : croire que x² = 2x. Faux et archi-faux !
Correctif : x² signifie x fois x ; rien à voir avec l’addition.
Erreur n°4 : Parenthèses fantômes – ces pièges qui font sauter la note
Exemple typique : -3(x-1), tu oublies d’appliquer le signe négatif à tout ce qui suit.
Correctif : Développe bien –3(x–1) = –3x +3.
Erreur n°5 : Simplifications interdites (ce qu’on ne peut JAMAIS barrer)
Certains croient malin de simplifier (x+4)/x en « 4 » ou « 1 ». Non, non et non.
Correctif : On ne barre jamais des additions/soustractions au numérateur et dénominateur sans facteur commun partout.
Erreur n°6 : Substitution bâclée – vérifier avant de remplacer
Tu remplaces trop vite la variable sans vérifier l’expression. Ex : Pour x = –1 dans 3(–1 + 2), certains écrivent “0” par flemme ou inattention…
Correctif : Remplace puis calcule étape par étape. Ici c’est 3×1=3.
Erreur n°7 : Rédaction mathématique bâclée (le détail qui sauve des points)
Écrire une ligne sur deux ou zapper les justifications. Résultat ? Tu comprends plus rien au bout de deux semaines et le prof t’allume en correction.
Correctif : Chaque étape posée, chaque transformation expliquée… sinon c’est retour CH6 sans passer par la case départ !
« Dans la vraie vie, ces erreurs t’attendent dès qu’il s’agit de budget ou codage – alors autant muscler ta rigueur maintenant que d’improviser sur tableur devant ton futur chef. »
Exercices corrigés de calcul littéral 4ᵉ : de la théorie à la pratique
Personne n’a jamais percé le code du calcul littéral en restant planqué derrière les exemples bidons des manuels à trous. Ici, c’est du vrai, du concret : tu passes sur le banc d’essai avec des exercices qui te grillent direct si tu fais semblant de piger.
Niveau initiation : 5 mini-défis pour poser les bases

Simplifie les expressions suivantes (corrigé juste après) :
1. $A = 4x + 3x - 2x$
2. $B = 2(y+5) + y$
3. $C = 5(x-1) - x$
4. $D = 3z + 7 - 2z + z$
5. $E = a + a + a - 2a$
Y’a pas plus basique – si tu coinces déjà là, revois d’urgence les fondamentaux.
Niveau intermédiaire : développer, réduire, factoriser sans filet

Chrono enclenché (max. 2 min / exo sinon t’as loupé la manip) :
- Ex1 : Développe puis réduis $(x+4)(x-2)$
- Ex2 : Réduis et factorise $6a + 9b -3a$
- Ex3 : Développe puis réduis $3(x+2)+5(x-1)$
Petit conseil : jamais vu un prof ne pas grincer des dents devant un signe oublié ou une parenthèse qui disparaît par magie…
Niveau expert : problèmes contextualisés (géométrie, physique)

- Rectangle mutant : Son aire s’exprime en fonction de x si sa longueur fait $(x+3)$ cm et sa largeur $(2x-1)$ cm.
- Calculer l’aire en fonction de x ; vérifier pour x=2.
- Voiture casse-la-dalle : Une tuture roule à v km/h pendant t heures.
- Donne l’expression de la distance D parcourue en fonction de v et t ; calcule D pour v=90, t=1,5.
Autant dire : si tu bloques ici… CH7/CH8 vont te broyer au contrôle !
Corrigés détaillés avec pièges commentés (ENTITES CH7/CH8)

Voici le raisonnement attendu pour chaque type d’exercice — et les boulettes fatales à traquer :
Corrigés rapides niveau initiation
- $A = (4+3-2)x = 5x$ ➡️ Erreur vue trop souvent: oublier de factoriser par x.
- $B = 2y +10 + y = (2y+y)+10 = 3y+10$
- $C = 5x-5-x= (5x-x)-5=4x-5$
- $D= (3z - 2z + z )+7 = (2z)+7$
- $E= a+a+a-2a=(3a-2a)=a$
Corrigés intermédiaire/avancé
- Ex1 : $(x+4)(x-2)= x^2+4x-2x-8=x^2+2x-8$. Piège: zapper un terme ou rater un signe négatif.
- Ex2 : $6a+9b-3a=(6a-3a)+9b=3a+9b=3(a+3b)$. Attention: oublier le facteur commun ou mal grouper !
- Ex3 :$3(x+2)+5(x−1)=3x+6+5x−5=(3x+5x)+(6−5)=8x+1$. Erreur classique: additionner/déduire au hasard.
Problèmes contextualisés
- Aire rectangle : $(x+3)(2x−1)=2x^2+x−3$. Pour x=2 : $(2+3)(4−1)=5×3=15$, vérifie aussi le développement obtenu ($4 imes 4 + 10 imes (-1)$... non terminé sinon).
- Boulette repérée: ne pas distribuer chaque terme ou remplacer avant d’avoir simplifié !
- Distance voiture :$D=v\times t$, ici $D=90\times1{,}5=135$ km.
- Piège typique: inverser les variables ou zapper une unité.
Erreurs détectées dans les copies :
* Parenthèses disparues mystérieusement (t’as cru qu’on jouait au loto ??)
* Signe négatif oublié dans le rush (coucou CH8)
* Variables confondues ($xy$ ≠ $x+y$)
* Simplification sauvage sans facteur commun partout (No go total)
* Substitution AVANT réduction — carton jaune assuré !
Fiches, vidéos et PDF gratuits pour réviser le calcul littéral
Autant vous dire : les fiches payantes et vidéos à rallonge, c’est la combine des plateformes pour te piquer ton temps et tes euros. Ici, place au pragmatique : téléchargements gratos, playlist sans minute perdue, ressources vérifiées – du vrai service public façon sniper.

Télécharger la fiche mémo PDF (cours + formules clés)
Fiche ultra-synthétique dispo sans inscription ici : FICHE METHODE CALCUL LITTERAL – PDF (zéro pub, zéro fioriture). Même ta grand-mère pourrait la relire avant le contrôle – pas d’arnaque, juste l’essentiel.
Playlist YouTube recommandée : 4 vidéos ciblées de 5 min
Pas de blabla inutile, que du concret — playlist pour ceux qui détestent perdre leur vie devant un prof endormi…
1. MATHEMATIQUES-4e- CALCUL LITTERAL – VIDEO D'EXERCICES (4:37)
2. Calcul littéral - 4e - Playlist YouTube (vidéos éclairs sur distributivité/réduction)
3. 4e Calcul littéral – Explications rapides
4. Le calcul littéral (Lumni) – version punchy
👍👍👍👍 pour playlist ‘mathix.org’ (rythme rapide, exercices corrigés en live, zéro décrochage).
Ressources premium… gratuites : sélection et critères de fiabilité
— Mathix.org: MAJ fréquentes, corrections détaillées par thèmes ; toutes les manip’s sont testées sur des élèves réels, rien d’obsolète ou généré par IA paresseuse.
— Maths à la maison : exercices interactifs régulièrement relus par des profs en activité — grande clarté visuelle et navigation rapide.
Critères retenus ? Zéro pub invasive, dernière mise à jour post-2022, corrigés accessibles dans la foulée — parce que pas moyen de bosser avec des ressources rouillées ou non corrigées.
Plan de révision express avant le contrôle (J-7 à J-0)
Autant vous dire, si tu crois que la révision s’improvise la veille, t’as déjà perdu la moitié du match. Ici, c’est planning béton, mémoire affûtée et zéro place pour le stress bidon.
Organiser la révision : planning et objectifs SMART
Ne laisse jamais les manuels te vendre l’illusion du "tout d’un coup". La clé ? Fractionner les notions sur une vraie semaine, pas sur une nuit blanche arrachée.
| Notion | J-7 | J-6 | J-5 | J-4 | J-3 | J-2 | J-1 | Jour J |
|---|---|---|---|---|---|---|---|---|
| Expressions littérales | ✔️ | Réactiver | ||||||
| Développement/réduction | ✔️ | ✔️ | ✔️ | |||||
| Distributivité/factorisation | ✔️ | ✔️ | ||||||
| Exercices corrigés | ✔️ | ✔️ | ✔️ | ✔️ | Correction | |||
| Quiz chrono/flashcards | ✔️ | ✔️ | ✔️ |
Objectifs : chaque session = 30 min max, en mode focus — pas de scroll Insta.
Techniques d’ancrage mémoriel : flashcards et quiz minute
Stop aux fiches-mur-de-Berlin ! Les cracks bossent avec des flashcards (type Quizlet ou à l’ancienne sur papier). Astuce qui déboîte : une question par notion/piège (« Développe 2(x+3) », « Explique différence entre x² et 2x »), réponse au dos. Le lendemain, tu recycles celles que t’as zappées.
Quiz minute : chrono en main, 5 questions-vérité à l’arrache sur ce que t’as vu la veille — rien de tel pour repérer les trous dans la raquette…
Surmonter le stress d’évaluation : check-list mentale jour J
- Relis les consignes AVANT d’écrire (ça paraît idiot… jusqu’à l’erreur de consigne)
- Prends 30 secondes pour lire TOUT le sujet avant d’attaquer la moindre question.
- Si tu bloques : saute direct à l’exercice suivant au lieu de bégayer dix minutes.
- Respire ! Personne n’a jamais explosé une note sous panique contrôlée.
Ressources liées pour aller plus loin (nombres relatifs, DM, autres matières)

Tu veux bétonner ton niveau au-delà du calcul littéral ? Fonce voir la page Cours nombres relatifs 4ᵉ, c’est le socle en ENTITES CH9 – addition, soustraction de nombres négatifs, tout est décortiqué sans sucre ajouté. Franchement, zapper ça avant un contrôle c’est comme oublier la base du burger : on passe à côté du goût et des points faciles.
Autres pistes solides (pas de lien cliquable ici) :
- Devoirs maison type Physique-Chimie (calculs d’énergie, formules à manipuler)
- QCM interactifs façon SVT (exprimer des résultats avec des variables)
- Exercices interdisciplinaires mêlant maths et techno
Soyons clairs : ceux qui bossent ces thèmes prennent une avance insolente sur la troupe. À toi de jouer.
Votre feuille de route pour cartonner en calcul littéral
Pas de blabla universitaire ni de promesses creuses : si tu veux exploser les scores en calcul littéral, joue-la sniper, pas touriste. Les maths, c’est pas un don, c’est du taf ciblé et une rigueur qui tue.
- Dégomme les automatismes idiots : Ne substitue jamais sans réfléchir, comprends toujours le sens derrière les lettres — sinon tu resteras au niveau "remplisseur de cases".
- Passe à l’action avec du vrai concret : Entraîne-toi sur des exos qui font mal, corrige tes plantages sans pitié et note chaque piège que t’as croisé (parenthèses, signes, distributivités ratées).
- Monte en puissance : Dès que ça roule sur le basique, attaque des problèmes plus corsés ou va voir des exercices avancés. C’est là que tu prends l’avantage sur la concurrence.
Ultime rappel : « Ne laisse pas ce que tu ne sais pas faire interférer avec ce que tu peux déjà réussir. » (John Wooden) – alors passe à l’acte. Plus tu pratiques smart, plus la victoire sentira la poudre…






