Prépare-toi à vivre l’expérience la plus satisfaisante de ta semaine : on t’explique (vraiment) le théorème de Thalès. On te montre comment l’utiliser pour calculer des longueurs, démontrer des parallélismes, et même comprendre le monde qui t’entoure. Le tout avec un minimum d’efforts. D’ailleurs, on t’offre même une astuce mnémotechnique qui t’évitera de l’oublier (ou de le confondre). Si tu pensais que ce truc était bon à jeter aux oubliettes, prépare-toi à changer d’avis.
Comprendre le Théorème de Thalès : Définition simple 📐
Personne ne m’a jamais dit qu’un jour, comprendre le théorème de Thalès serait aussi simple que mesurer un banc avec une latte. Et pourtant, soyons clairs : Thalès, c’est le couteau suisse mathématique pour comparer des longueurs dès qu’apparaissent des droites parallèles et sécantes. Rien d’ésotérique ici : il s’agit juste de savoir faire le lien entre les mesures d’un dessin—et pas seulement sur du papier quadrillé !
Le théorème de Thalès, c’est la simplicité qui se cache derrière l’apparence sophistiquée des manuels : du pur rapport logique.
Ce qu'est réellement le Théorème de Thalès
Dans la vraie vie, le théorème dit ceci : Si tu as deux droites qui se coupent (on dit "sécantes" pour épater la galerie) et que deux autres leur tombent dessus en restant bien parallèles, alors les longueurs des segments que tu obtiens sont dans un rapport égal entre elles. Autant vous dire, c’est plus utile qu’un parapluie à Marseille.
Au lieu de balancer des mots compliqués, on pourrait simplement dire : "Tu veux mesurer une distance inaccessible ? Trace des parallèles, mesure ce qui est accessible, applique Thalès." C'est tout.
Les conditions pour parler de 'situation de Thalès'
Attention ! On n’utilise PAS ce théorème n’importe comment (même si ça arrangerait bien certains). Il faut strictement :
- Deux droites dites sécantes (qui se croisent en A) — appelons-les (AB) et (AC), histoire d’éviter les embrouilles.
- Deux droites parallèles, typiquement notées (BC) et (DE), qui coupent nos deux sécantes en B/C et D/E respectivement.
- Les points doivent être bien rangés dans le même ordre sur chaque droite, sinon tout s'effondre.
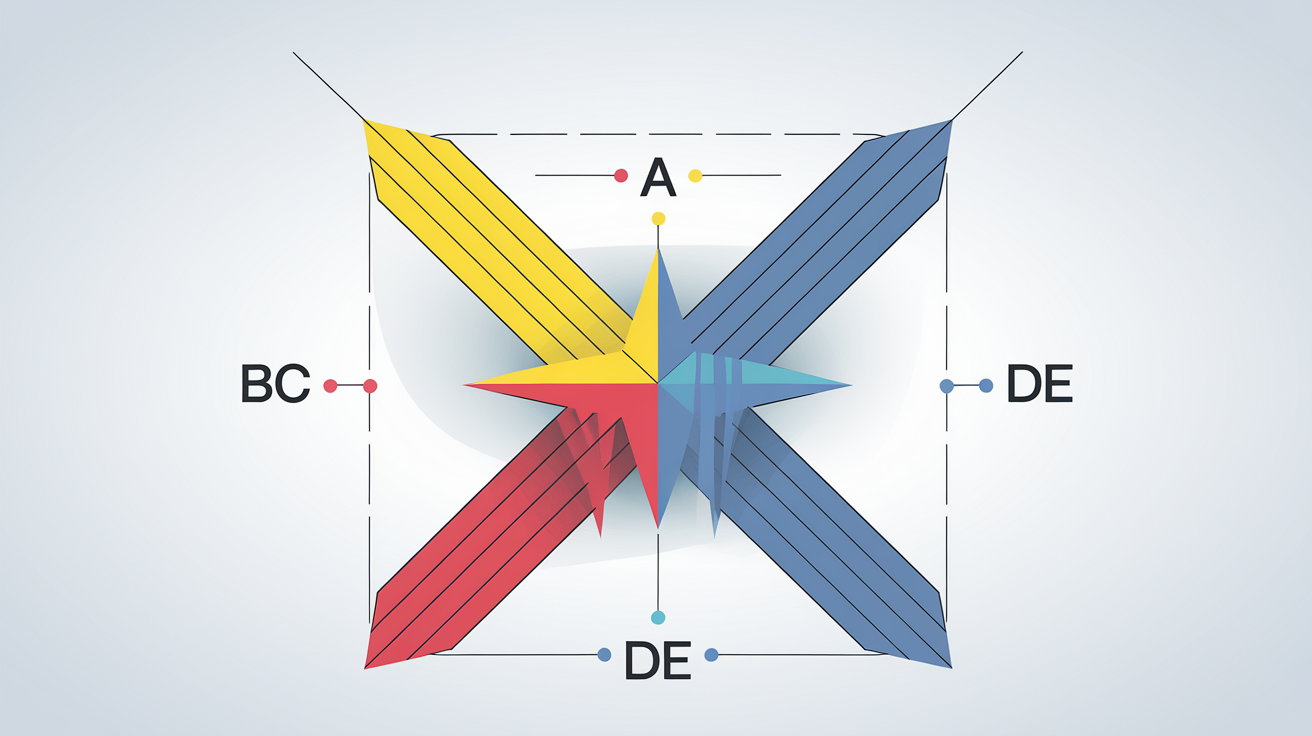
Ce schéma aurait dû figurer dans tous les cahiers… mais visiblement certains préfèrent brouiller les pistes.
La formule du Théorème de Thalès expliquée simplement
La formule canonique qui fâche ou illumine selon les cas :
AB/AD = AC/AE = BC/DE
Traduction sans ampoule au plafond :
- AB et AD sont sur la même sécante (prolongée depuis A vers B et D)
- AC et AE idem sur l’autre sécante (A vers C et E)
- BC et DE sont sur les parallèles !
Prenons un exemple minable mais efficace : si AB = 3 cm, AD = 6 cm, alors tout segment sur l’autre branche devra respecter la proportion suivante. Si AC = 4 cm alors AE doit être 8 cm (car 3/6 = 4/8).
Astuces pour ne plus confondre ou oublier le Théorème de Thalès 🚀
On ne va pas tourner autour du pot : si tu confonds encore Thalès avec une recette de grand-mère, c’est que personne n’a daigné t’offrir les seuls vrais trucs qui marchent. Je balance donc sans filtre :
Astuces mnémotechniques pour mémoriser facilement
- La colonne de gauche, la colonne de droite : Écris toujours les segments sur la même sécante dans la même colonne. Les colonnes guident tes rapports comme des rails.
- Le papillon : Trace la figure en forme de "X" (les deux sécantes), superpose les droites parallèles… Résultat ? Deux ailes identiques, chaque aile hébergeant un rapport égal. Visuel, implacable.
- Tourne toujours dans le même sens : Lis ta figure dans l’ordre A vers B puis A vers D, puis passe à l’autre branche (A vers C puis A vers E). Même boucle logique pour chaque proportion.
- Rapport = même ordre sinon carnage : Les segments doivent respecter l’ordre des points ; on ne mélange pas tout sous prétexte qu’on est pressé pour la cantine !
- Un jeu de mots idiot : “Parallèles = Proportionnelles”, tu colles ça partout et ton cerveau fera le boulot la nuit.
Identifier une situation de Thalès dans un dessin
Soyons clairs : il s’agit de repérer deux droites qui se croisent bien proprement (point d’intersection net) et deux droites qui sont vraiment parallèles (pas « à peu près »). Trois points alignés sur chaque sécante—sinon c’est mort. Si au moindre doute tu dois plisser les yeux pour deviner les parallèles, c’est NON !
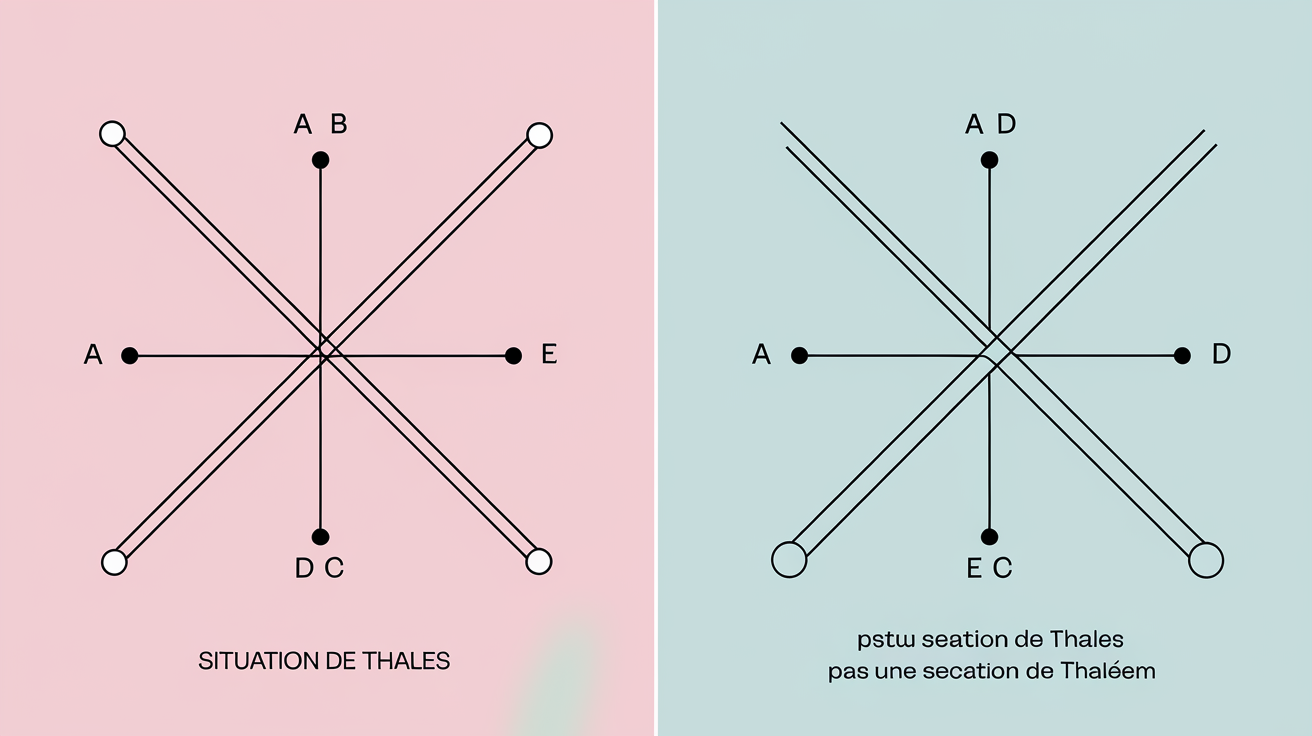
À gauche, tout respire la géométrie saine : sécantes franches, parallèles parfaites. À droite… non-recevoir ! Parallèles tordues, points mal alignés = zéro Thalès.
J’ai vu un prof distribuer du Thalès à tout propos — résultat ? Une classe entière à coller des rapports là où il n’y a même pas d’égalité possible. Ce n’est PAS automatique, c’est chirurgical. Lève les yeux, vérifie l’alignement et le parallélisme avant toute chose.
Les erreurs courantes à éviter
- Confondre les segments utilisés dans les rapports (mettre AB/AC alors que c’est AB/AD)
- Oublier la vérification des droites parallèles (une approximation au crayon ne suffit pas)
- Viser une configuration « qui ressemble » mais qui ne respecte pas l’alignement strict
- Mal identifier le point d’intersection principal (« A » souvent appelé centre), ce qui flingue toute ta démonstration
- Appliquer bêtement la formule sans regarder si chaque rapport correspond bien à des longueurs comparables sur la figure
Autant vous dire, on ne compte plus ceux qui tombent dans ce trou noir tous les ans !! Soyons collectivement moins crédules.
Le Théorème de Thalès : Un outil toujours indispensable 💡
On va couper court aux idées reçues : Thalès, c’est pas le vinyle collector qu’on expose pour faire joli. C’est l’outillage universel des mathématiques appliquées, toujours au top dans la vraie vie, dès qu’il faut comparer des longueurs ou vérifier si deux droites jouent franc jeu. Même les concours les plus corsés n’osent pas le snober, c’est dire !
Si tu veux comprendre la géométrie moderne, résoudre des problèmes complexes et progresser en mathématiques avancées, maîtrise le Théorème de Thalès.
Les 3 raisons majeures pour lesquelles Thalès reste crucial :
- Il permet le calcul de longueurs inaccessibles dans toutes sortes de configurations (bâtiments, cartes, modèles).
- Il sert à prouver le parallélisme et donc à valider ou invalider des situations géométriques réelles ou théoriques.
- Il est la base logique d’une foule de théorèmes plus sophistiqués (affines, projectifs…), et le meilleur sésame pour qui veut survivre en géométrie avancée.
Autant vous dire : tu veux faire carrière en maths ou juste ne pas passer pour une buse ? Maîtrise Thalès. C’est le ticket d’entrée—pas négociable.






