On est tombés sur un article qui affirme que la convexité est "la notion la plus importante des mathématiques". Parfois, l’hyperbole est nécessaire pour approcher la vérité. Car soyons clairs : en termes de puissance analytique, de profondeur conceptuelle, d’universalité et d’applications, ce concept est sans égal. Mais cette force est aussi sa faiblesse : tant qu’on ne l’a pas apprivoisé, il peut sembler obscur, contre-intuitif et rébarbatif. Résultat : 90% des étudiants le fuient comme la peste. Alors qu’il suffit de l’aborder sous le bon angle pour en faire un allié redoutable. Voilà pourquoi on prépare un guide ultra-complet pour comprendre, démontrer et appliquer les inégalités convexes/concaves. Ce qui t’attend : - 10+ inégalités incontournables (Jensen, Hölder, Gibbs…) - Les méthodes de preuve qui rapportent des points - Des applications concrètes en maths et en physique - Un exercice corrigé interactif - Les erreurs et pièges à éviter - Des ressources pour creuser en autonomie. Prépare-toi à découvrir la notion la plus puissante (et fascinante) des maths.
Inégalités convexes vs concaves : l’essentiel en 30 secondes ⏱️
Résumé express des définitions
- Fonction convexe : Entre deux points du graphe, la courbe passe SOUS la corde (autant vous dire, c’est la base à ne pas rater).
- Fonction concave : Cette fois, la courbe passe dessus — c’est l’inverse (qui se trompe encore ? Beaucoup trop...).
- Sens de l’inégalité : Convexe = f(λx₁+(1−λ)x₂) ≤ λf(x₁)+(1−λ)f(x₂), Concave = le signe ≥.
- Teaser Jensen : La superstar qui va venir casser vos certitudes sur les moyennes.
Tableau comparatif sens des inégalités
| Type | Condition analytique | Exemple canonique | Tendance géométrique |
|---|---|---|---|
| Convexe | f(λx₁+(1−λ)x₂) ≤ λf(x₁)+(1−λ)f(x₂) | exp(x), x² | Sous la corde, bombée vers le haut |
| Concave | f(λx₁+(1−λ)x₂) ≥ λf(x₁)+(1−λ)f(x₂) | ln(x), racine carrée | Au-dessus de la corde, creusée vers le bas |
Astuce tech : Pour écrire ça proprement en concours ? MathJax ou LaTeXML – sinon vous pleurez sur Word.
Pourquoi ça obsède les examinateurs ?
Soyons clairs, la convexité c’est l’arme fatale des concepteurs de sujets MINES & ECG. Ça se glisse partout : inégalités, optimisation, proba et même thermodynamique. Les applications sont tentaculaires et l’étudiant qui ne manie pas ces notions est condamné à ramasser les miettes… et à refaire un tour au lycée mentalement.
Je crois fermement que 90 % des étudiants confondent encore convexe et concave à cause d’un mauvais schéma en seconde.
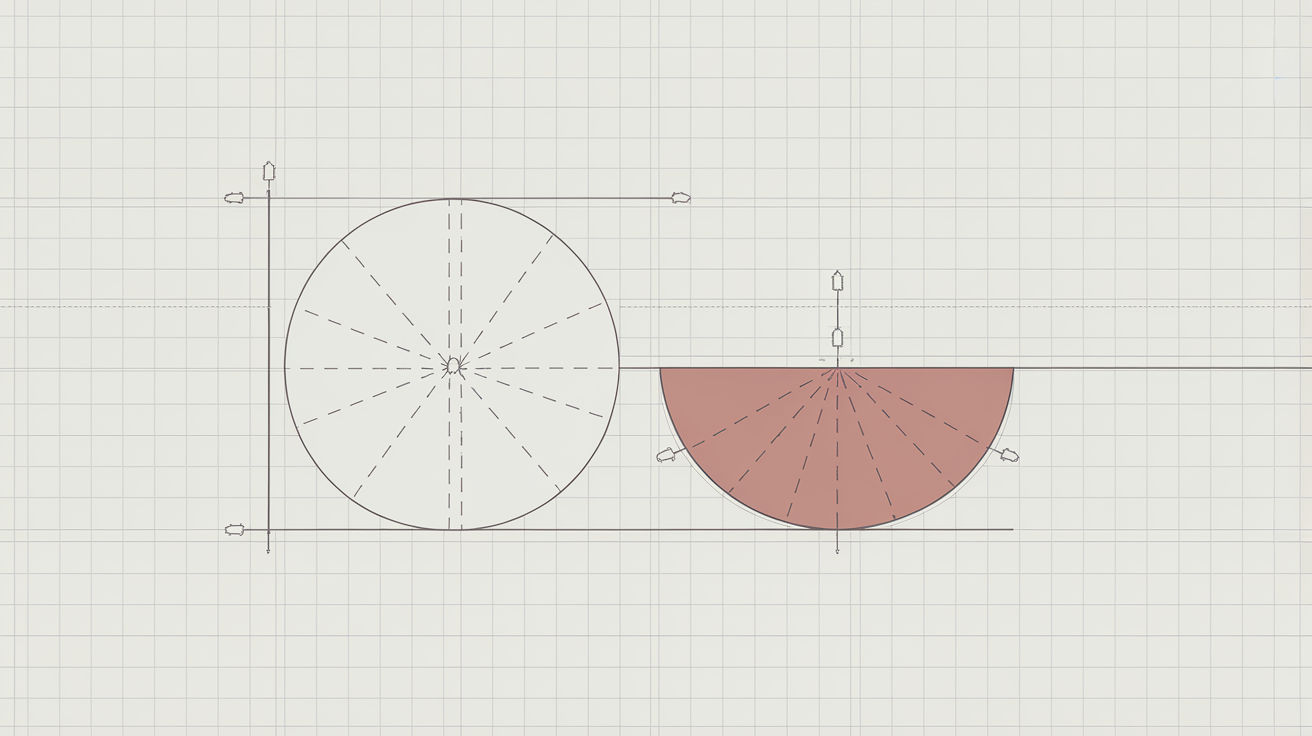
Convexité et concavité : définitions rigoureuses et intuition géométrique
Combinaisons convexes : le cœur du sujet
Soyons clairs : si tu ne maîtrises pas la notion de combinaison convexe, tu te tires une balle dans le pied pour tout ce qui suit. Une combinaison convexe entre deux points x₁ et x₂, c’est simplement λx₁ + (1−λ)x₂, où λ est compris entre 0 et 1. Et crois-moi, ce lambda-là ne dort jamais ! Il te poursuit des probabilités à l’optimisation — un vrai stalker mathématique.
Autant vous dire, même B. Legat (le type qui t’étrille en oral Mines) n’attend qu’une chose : que tu zappes de penser à λ comme à un poids qui fait le barycentre entre tes deux points. C’est la règle d’or du jeu — tous les coefficients positifs ET leur somme vaut 1, sinon c’est open bar et plus rien n’a de sens.
Visualiser : cordes, tangentes et courbure
Arrête de croire que l’intuition c’est pour les faibles ! Dans la vraie vie, la convexité se lit sur la position de la courbe par rapport à la droite reliant deux points (la fameuse corde). Pour une fonction convexe, le graphe reste toujours SOUS cette corde — aucune triche possible. Pour les puristes (et ceux qui aiment souffrir), retiens aussi : toute tangente à la courbe reste EN DESSOUS du graphe sur l’intervalle concerné.
Et là où ça pique (mais c’est génial), c’est que mathématiquement, une fonction f est convexe sur un intervalle dès que sa dérivée seconde est positive partout sur cet intervalle… Mais ATTENTION : il existe des fonctions convexe sans dérivée seconde — donc ne ronfle pas sur cet indice !
Exemples canoniques : exp, ln, x²
Si tu veux briller (ou juste survivre), retiens ces trois là :
- exp(x) : Dérivée seconde = exp(x) > 0 partout – c’est LA Rolls-Royce de la convexité. Toujours bombée vers le haut, impossible d’y échapper.
- ln(x) : Dérivée seconde = -1/x² < 0 sur ℝ₊* – star absolue de la concavité. On veut souvent piéger avec elle en TD.
- x² : Dérivée seconde = 2 > 0 – l’élève modèle-convexe que même MathTraining utilise en intro tellement il coche toutes les cases.
Les étudiants qui arrivent à confondre exp et ln niveau convexité… finissent généralement blacklistés par les correcteurs Mines-Ponts. À méditer !
Critères analytiques pour détecter la convexité ou la concavité
Dérivée première croissante/décroissante
Soyons clairs : si tu veux flairer la convexité sans te prendre les pieds dans le tapis, il faut regarder du côté de la dérivée première. Une fonction f est convexe sur un intervalle si sa dérivée f′ est croissante. Oui, croissante ! Et pour la concavité ? Tout l’inverse, f′ décroissante. Dans la vraie vie, ça veut dire que plus tu avances, plus la pente grimpe (ou au moins stagne), pas d’entourloupe.
- 🔍 Si f′ croît ⇒ f convexe
- 🔍 Si f′ décroît ⇒ f concave
- 🔍 Affine (f′ constante) ⇒ à la fois convexe et concave (luxe rare...)
Intuition graphique : imagine la pente d’une rampe de skate qui devient de plus en plus raide — c’est ça une convexe. Ceux qui zappent ce critère finissent par empiler les contresens.
Dérivée seconde positive/négative
Autant vous dire, on va pas faire dans le coton. Si f est deux fois dérivable, alors :
- f″(x) ≥ 0 sur l’intervalle ⇒ f est convexe ;
- f″(x) ≤ 0 ⇒ concave.
Preuve expresse, façon N. Radu :
Quand f''(x) ≥ 0, alors la variation de f' est non négative, donc la pente ne décroit jamais ; déballage intégral : pour tout x < y,
f'(y) - f'(x) = ∫ₓʸ f''(t) dt ≥ 0… donc f'(y) ≥ f'(x). Convexité validée sans anesthésie.
Et maintenant ? Retenez-le au marqueur indélébile : dérivée seconde positive = courbure vers le haut. Mais certains n’ont jamais vérifié les hypothèses – méfiance sur les points où c’est non défini !
Hessienne et cas multivarié
Passons au level supérieur : plusieurs variables ? Alors on regarde la matrice Hessienne (matrice des dérivées secondes partielles). La règle ?
- La fonction est convexe sur un ouvert Ω ⊂ ℝⁿ si sa Hessienne H(x) est positive semi-définie (PSD) partout sur Ω.
- En clair : pour tout vecteur v ≠ 0, vᵗ Hv ≥ 0.
- Mini-exemple cash : f(x,y)=x²+y². Sa Hessienne ? Matrice diag(2,2), toujours >0 donc ultra-convexe.
Astuce : On trouve souvent des cas où strictement convexe ≠ Hessienne strictement définie positive partout. Eh oui — piège classique des concours !
Contre-exemples qui piègent
Dans la vraie vie, il existe DES FONCTIONS CONVEXES QUI NE SONT PAS DÉRIVABLES PARTOUT ! Combien tombent encore dans le panneau…
- f(x) = |x| : Convexe mais non dérivable en x = 0. À chaque oral Mines-Ponts y’en a un qui se loupe dessus !
- f(x) = max(0,x) : Pareil, coin anguleux en zéro mais on reste dans le club des convexes.
Les étudiants trop pressés « d’intégrer » oublient que convexité n’implique PAS différentiabilité – preuve qu’on ne révise jamais assez les fondamentaux.
Panorama des inégalités liées à la convexité
Inégalité de Jensen : énoncé, preuve, cas d’égalité
Soyons clairs : l’inégalité de Jensen, c’est le boss final de la convexité. Pour toute fonction convexe $f$ et pour des poids positifs $\lambda_i$ qui font $\sum \lambda_i = 1$ (c’est pas optionnel), tu as:
$$f\left(\sum \lambda_i x_i\right) \leq \sum \lambda_i f(x_i)$$
La preuve sans moulinette ? Prends deux points $x_1, x_2$, regarde la tangente en $x_1$ : elle reste SOUS le graphe par convexité. Fais glisser ton $\lambda$ dans $[0,1]$, tu obtiens la corde — et la fonction ne dépasse JAMAIS la corde ! Donc l’inégalité est validée pour n’importe quelle combinaison.
Cas d’égalité ? Il y en a un seul qui tient debout : lorsque $f$ est affine sur l’intervalle (ou que tous les $x_i$ sont égaux). Les autres qui bricolent là-dessus se font recaler à chaque oral sérieux.
Retenez : une démo façon «pente de la tangente» rapporte plus qu’un baratin appris sur Wikipédia…
Hölder & Minkowski : le duo choc
Dans la vraie vie, ceux qui récitent Cauchy-Schwarz sans jamais citer Hölder se privent du level-up analytique. L’inégalité de Hölder dit :
$$\left( \sum |a_i b_i| \right) \leq \left( \sum |a_i|^p \right)^{1/p} \left( \sum |b_i|^q \right)^{1/q}$$
pour $p>1$, $q$ son conjugué ($1/p + 1/q = 1$). La démonstration sérieuse ? C’est une histoire de convexité via l’exponentielle ou, encore mieux, de concavité du log (voir BibMath). Le clin d’œil recette concours : factorisez un lambda malin dans les puissances pour voir surgir Jensen en coulisse !
Quant à Minkowski (le cousin discret), il te garantit que $$||x+y||_p \leq ||x||_p + ||y||_p$$ — exactement comme une trochinette triangle mais version espaces L^p. Les ignorants qui ne comprennent pas l’origine convexe derrière ces inégalités déçoivent systématiquement en grand oral.
Inégalité de Gibbs et entropie
Là on atteint le graal : l’entropie et Gibbs. L’inégalité de Gibbs s’écrit souvent $$-\sum p_i \ln q_i \geq -\sum p_i \ln p_i$$ quand $(p_i)$ est une loi de proba et $(q_i)$ aussi. Pourquoi ? Car $-\ln x$ est convexe ! Toute l’info-théorie moderne (codage optimal, analyse big data…) descend direct de cette propriété. Ceux qui pigent ça voient les liens entre statistiques et convexité partout… Normal : c’est tout le secret du « minimum d’entropie ».
Moyenne arithmético-géométrique revisitée
AM ≥ GM — ceux qui ne savent pas prouver ça via Jensen sur $f(x)=\ln x$, franchement… Le raisonnement béton : applique Jensen avec poids égaux, tu as $$\ln\left(\frac{a_1+...+a_n}{n}\right) \geq \frac{1}{n}\sum_{i=1}^n \ln a_i,$$
d’où AM ≥ GM après exponentiation !
Je parle aux vrais : rien n’égalera ce shoot espresso mathématique qu’on ressent quand on recase AM ≥ GM avec Jensen devant un examinateur sec comme un vieux polycopié.
Méthodes de démonstration : recettes anti-sèches de concours
Technique de la droite de soutien
Les examinateurs MP raffolent du mot "droite de soutien", mais 95% des candidats ne savent pas le tracer ! Soyons clairs : une droite de soutien à une fonction convexe $f$ en $x_0$ est une droite qui passe par $(x_0, f(x_0))$ et reste SOUS le graphe sur tout l’intervalle. Déroulé minute :
1. Fixe un point $x_0$ où $f$ est dérivable (sinon tu cries « cas anguleux »).
2. Calcule la tangente : $y = f(x_0) + f'(x_0)(x-x_0)$.
3. Vérifie : pour tout $x$, $f(x) \geq f(x_0) + f'(x_0)(x - x_0)$.
C’est LE critère qui fait mouche dans les sujets d’oraux Mines/MP ! Et comme le programme MP insiste là-dessus, attends-toi à devoir justifier pourquoi toute fonction convexe possède au moins UNE droite de soutien en chaque point intérieur (hors cas patho).
Concaténation de Jensen
Voici la version pour vrais snipers : pour généraliser Jensen à n arguments, il suffit d’enchaîner l’inégalité sur les paires successives, façon domino. Prends $n=3$ et fais-le deux fois :
- D’abord entre $x_1$ et $x_2$, puis entre le résultat et $x_3$, avec ajustement des poids.
- À chaque étape, vérifie que la somme des lambdas reste 1 (sinon c’est la sortie directe…).
Tu peux rédiger ça proprement en LaTeXML ou MathJax, histoire d’impressionner le jury qui corrige au format .tex uniquement.
Passage discret → continu
Le passage du cas sommé (discret) à l’intégré (continu), c’est là où tout le monde se prend les pieds dans le tapis. Le principe ? Prendre la limite quand le nombre d’arguments tend vers l’infini : $$\lim_{n\to \infty} \sum_{i=1}^n \lambda_i f(x_i) \rightarrow \int_a^b f(x)\,d\mu(x).$$ Les profs attendent que tu cites Riemann ou Lebesgue « pour briller ». Notations propres avec MathJax obligatoire sinon tu finis en mode brouillon !
Astuces pour factoriser un lambda
Voici la checklist hacks que tu dois avoir tatouée sur ta main gauche :
1. Sortir les λ communs dans toute somme pondérée avant d’appliquer Jensen.
2. Changer d’ordre de sommation pour exploiter symétrie ou regroupement malin des λ.
3. Remplacer λ par 1–λ dans les preuves à deux variables — certains oublient ce réflexe simple qui fait gagner du temps !
🛠️ Ces trois moves suffisent à éviter 80% des plantages en khôlle.
Applications concrètes : de l’optimisation à la théorie de l’info
Programmation convexe et recherche opérationnelle
Soyons directs : la programmation convexe écrase tout le reste quand il s’agit de garantir un optimum global sans te retrouver piégé par des minima pourris. Si ton objectif et tes contraintes sont convexes, chaque solution locale = globale, point final. Dans la vraie vie ? Portefeuille de Markowitz, allocation de ressources en logistique — tous les modèles sérieux utilisent ça pour éviter les plantages industriels. Le framework Bootstrap (oui, le fameux pour habiller tes interfaces Web) permet même aux étudiants d’expérimenter visuellement des surfaces convexes, avec sliders et rendu instantané : impossible de faire plus concret pour saisir comment converge une optimisation propre.
Probabilités : espérance & variance sous contrôle
Dans le monde réel, Jensen n’est pas qu’un gadget pour concours : c’est LE garde-fou sur E[f(X)] ≥ f(E[X]) dès que f est convexe. Exemple qui tue ? Prends f(x)=x² — tu retrouves direct que Var(X) = E[X²] - (E[X])² ≥ 0… juste parce que x² est convexe ! Ceux qui ne voient pas la portée probabiliste vivent dans la préhistoire mathématique.
Machine learning : pourquoi les loss sont convexes
On ne va pas tourner autour du pot : sans convexité des fonctions de perte (log-loss, hinge pour SVM, MSE…), la backprop finirait à l’hospice. La raison ? Avec une fonction convexes, tu fais confiance à l’algo d’optimisation— chaque descente de gradient te dépose direct au minimum global, zéro drame local ! Autant vous dire, le GPU aime la convexité : entraînement stable, convergence rapide. Ceux qui se pavanent avec des modèles non convexes doivent aimer souffrir ou veulent juste cramer du watt inutilement.
Thermodynamique : entropie et irréversibilité
Là où les candidats se font hacher menu ? Le lien entre convexité/concavité et entropie. En vrai, l’entropie S(U) est typiquement concave en thermodynamique mais ses transformées (style Legendre) réapparaissent sous forme convexe dans les potentiels thermo — et c’est là que Gibbs débarque. La concavité garantit que toute fluctuation fait grimper le désordre (flèche du temps = aucun retour en arrière). Ne confondez plus micro-vagues de proba et macro-irreversibilité : tout se joue sur ces propriétés mathématiques fines !
Ressources et bibliographie pour creuser sans sombrer
Livres de référence indispensables
- Convex Optimization – Stephen Boyd & Lieven Vandenberghe : la Bible du genre. Le seul livre que même les chercheurs en machine learning gardent sous le coude (PDF gratuit sur le site Stanford).
- Mathematical Analysis – Tom M. Apostol : pas spécifique convexité, mais incontournable pour les bases analytiques sérieuses.
- Pour ceux qui veulent la version old-school : Rockafellar, "Convex Analysis" — lecture indigeste mais t’apprends à encaisser.
Cours en ligne, MOOC et vidéos
- StanfordOnline: Convex Optimization (Boyd) – env. 6 semaines, niveau avancé (EN).
- MyMooc: Convex Optimization – durée : variable, tout public qui veut du solide.
- Chaîne YouTube : LE COURS : Convexité - Terminale (Yvan Monka, 30 min). Pas que pour les nuls…
Bases d’exercices interactifs
Pour arrêter de gober des définitions sans jamais se salir les mains :
- MathTraining : base ultra-ciblée sur convexité, avec corrigés détaillés — aucun autre site ne te pose des pièges aussi vicieux !
- Khan Academy : interface propre et quiz à volonté ; pas de blabla inutile mais efficace en mode drill.
Outils logiciels : GeoGebra, Python & Co.
Faut vivre avec son temps :
- CVXPY (Python) : modélisation d’optimisation convexe en deux lignes — aucune excuse pour ne pas tester tes idées !
- GeoGebra : visualise tous tes schémas convexes comme un crack, outils gratuits.
- Bootstrap : stylise tes graphiques d’optimisation si tu veux rendre tes exposés moins moches qu’un polycopié gribouillé.
Ceux qui s’arrêtent à Word+TI84 n’ont rien compris à la vraie vie maths moderne.
Morale de l’histoire : ce que la convexité dit vraiment sur nos certitudes
Soyons clairs : croire que la convexité n’est qu’une histoire de courbure, c’est rater tout l’enjeu. Le vrai pouvoir, c’est d’apprendre à distinguer l’apparence du fond, à séparer les raisonnements qui tiennent la route des illusions qui s’effondrent.
Dans la vraie vie, une idée « convexe » résiste toujours mieux aux secousses – parce qu’elle repose sur un mélange solide, pas sur des extrêmes isolés. Les étudiants qui ne voient pas plus loin que le graphe sont condamnés à refaire les mêmes erreurs, ad vitam…
La convexité n’est pas qu’une courbure, c’est une discipline mentale : savoir composer sans céder aux extrêmes, structurer ses idées pour viser l’équilibre et la robustesse !






