La transformée de Laplace est un outil incontournable pour les ingénieurs. Pourtant, elle reste souvent mal comprise en raison d'idées reçues, de pédagogies inadaptées et d'un manque de pratique. Voici un guide complet pour tout comprendre : explications, formules, exemples, mode d’emploi et pièges à éviter. La transformée de Laplace, c’est un peu le couteau-suisse des sciences appliquées. Grâce à elle, l’ingénieur peut modéliser, analyser et résoudre en quelques lignes ce qui lui prendrait des pages entières avec d’autres méthodes. Le problème ? Entre idées reçues ("c’est pour les génies barbus"), pédagogies bancales et manque de pratique, elle est aussi l’une des techniques les plus mal comprises et maîtrisées de la boîte à outils. Alors on a décidé de remédier à tout ça avec un guide ultra-complet. Au programme :
- Définitions et principes fondamentaux
- Bénéfices et cas d’usages
- Formules et tables de calcul
- Mode d’emploi pas-à-pas
- Applications terrain
- Pièges et limites
- Outils et ressources
- FAQ Le tout avec des exemples concrets et des cours vidéo en bonus. Si vous deviez apprendre une seule chose cet été, c’est celle-ci.
À quoi sert vraiment la transformée de Laplace ? 5 bénéfices immédiats pour vos équations
Oubliez les barbes poudrées et les regards fuyants des polytechniciens : la transformée de Laplace, c’est l’arme fatale des matheux pressés ET des ingénieurs pragmatiques. Pas besoin d’adorer les intégrales pour apprécier ce couteau suisse qui fait passer vos équations différentielles du stade « montagne infranchissable » à « trottoir praticable ». Autant vous dire : celui qui n’en profite pas aime souffrir !
Lineariser sans anesthésie : convertir une équation différentielle en algèbre
Vous rêvez de transformer une vilaine équation différentielle en une simple équation algébrique ? La magie opère avec l’opérateur p (ou s, selon la mode). Voici comment ça se passe, sans enfumage inutile :
- On applique la transformée de Laplace à toute l’équation (chaque terme, sans exception).
- Les dérivées deviennent polynomiales en p (exemple : d²y/dt² → p²Y(p)). C’est fluide comme une bière tiède.
- On résout l’équation algébrique obtenue puis on fait le retour dans le monde réel par inversion.
En trois coups de cuillère à pot, un problème non linéaire du temps passe au régime « solvable par Excel » sans anesthésie ni doliprane.
Gérer les régimes transitoires (élec, méca) sans suer
Dans la vraie vie, le régime transitoire fout souvent le bazar dans vos calculs électroniques ou mécaniques. Avec Laplace, pas de panique : il suffit de bosser dans le domaine complexe puis d’appliquer la convolution pour obtenir la réponse à n’importe quelle excitation.
- Plus besoin de jongler entre solutions générales et particulières : tout se gère dans le même sac !
- Le passage au régime établi est naturel, comme un vieux diesel qui finit par tourner rond.
🎯 Le gain de temps pour l’ingénieur est indéniable : 5/5.
Diagnostiquer un système LTI grâce à la fonction de transfert
Soyons clairs : pour un système LTI (linéaire invariant dans le temps), la fonction de transfert, c'est simplement le rapport entre la sortie et l'entrée dans le domaine de Laplace (H(p) = Y(p)/E(p)). Elle contient toute l’ADN du système — stabilité, résonance, réponse impulsionnelle… c’est ECB et carte vitale en une seule formule !
- Cette fonction permet d’analyser directement les comportements en fréquence et d’anticiper les réactions à n’importe quel stimulus.
- Anecdote terrain : Un industriel automobile m’a déjà confié que diagnostiquer un amortisseur sans passer par H(p), c’est aussi moderne que réparer une Tesla avec un burin.
Connecter temps et fréquence mieux qu’une FFT
La transformée de Fourier c’est sympa… mais limitée. La transformée de Laplace généralise en prenant en compte aussi bien les exponentielles décroissantes que sinusoïdales. Résultat ? Analyse complète des signaux causaux ET non causaux, là où Fourier ne traite que les signaux stationnaires. Bref : Laplace > Fourier au pays des systèmes dynamiques réels.
- Un détail qui tue : en évaluant sur l’axe imaginaire pur (p = jw), on retrouve exactement la transformée de Fourier !
Bonus probabilités : flairer la loi derrière la variable aléatoire
Pour ceux qui croient que Laplace ne sert qu’en automatique ou en élec : raté ! Côté probabilités, sa version s’appelle fonction génératrice des moments ou encore transformée de Laplace d’un random variable X (LX(t) = E(e^{tX})).
- Elle permet d’identifier plus vite qu’un Comité Nobel si vous avez affaire à une loi exponentielle ou gamma sous le capot statistique.
- Et elle supplante parfois même la « fonction caractéristique » classique selon les usages, notamment quand vous travaillez sur des queues épaisses ou des ruptures brutales.
La boîte à outils : formule, abscisse de convergence et table usuelle à garder sous le coude
Alerte aux dogmes poussiéreux : la transformée de Laplace n’a rien d’un mythe cérébral pour profs en chaussons. Voici l’essentiel, version terrain, pour la manipuler sans finir interné.
La formule intégrale officielle (et ses conditions MECE)
Autant vous dire : il n’existe aucune magie noire – juste une intégrale redoutablement efficace, à condition de piger où elle converge. Pour une fonction f(t), définie pour t ≥ 0 :
$$
F(p) = \int_0^{+\infty} f(t) e^{-pt} \, dt
$$
Le tout fonctionne si f(t) est localement intégrable et d’ordre exponentiel (sauf cas pathologique, mais bon courage pour tomber dessus sans le vouloir).
La convergence dépend de la partie réelle de p :
| Condition sur f(t) | Conséquence sur Re(p) | Commentaire |
|---|---|---|
| $ | f(t) | \leq Me^{a t}$ (M, a > 0) | $Re(p)>a$ | Cas standard des signaux physiques |
| $f$ bornée, support fini | $Re(p)>-\infty$ | Converge partout sauf pathologie |
| Croissance plus rapide qu’exponentielle | Ne converge nulle part | Cas purement théorique (inutile ici!) |
Déterminer l’abscisse de convergence sans s’arracher les cheveux
Soyons clairs : calculer l’abscisse de convergence revient à détecter la frontière au-delà de laquelle l’intégrale diverge façon geyser. Méthode ?
1. Majorez $|f(t)|$ par $Me^{at}$.
2. L’intégrale $$ \int_0^{+\infty} e^{-(p-a)t} dt $$ ne converge que si $Re(p)>a$.
3. Exemples qui claquent :
- Pour $f(t)=e^{2t}$ : $
F(p)=\int_0^{+\infty} e^{2t}e^{-pt}dt=\int_0^{+\infty}e^{-(p-2)t}dt$
$
pour $Re(p)>2$, donc $[1mσ_0=2[0m$.
- Dès que ça dépasse ce seuil : rideau, plus personne ne répond!
Table express des transformées usuelles (PDF & clic droit)
Pas le temps ni l’envie de fouiller trois manuels ? Voici l’essentiel qui marche partout et tout le temps, même à 3h du mat' avant un rendu Matlab.
| Fonction temporelle | F(p) | Domaine de validité |
|---|---|---|
| $1$ | $1/p$ | $Re(p)>0$ |
| $e^{at}$ | $1/(p-a)$ | $Re(p)>a$ |
| $sin(\omega t)$ | $\omega/(p^2+\omega^2)$ | $Re(p)>0$ |
| $cos(\omega t)$ | $p/(p^2+\omega^2)$ | $Re(p)>0$ |
| Dirac ($\delta(t)$) | $1$ | pour tout p |
Pour les insomniaques ou les maniaques du détail, table complète en PDF.
Lien interne : le parallèle éclair avec la Formule de Taylor-Young (/node/3128)
Envie d’aller plus loin ? Le développement limité donne une intuition locale là où Laplace regarde « toute » l’évolution temporelle – deux outils complémentaires pour dompter fonctions tordues et phénomènes dynamiques. L’astuce qui tue : chaque terme du développement limité se retrouve dans la série de puissances du développement de Laplace ! Pour creuser le lien profond : Développement limité et intuition locale.
Mode d’emploi pas-à-pas : résoudre une équation différentielle linéaire avec la méthode de Laplace
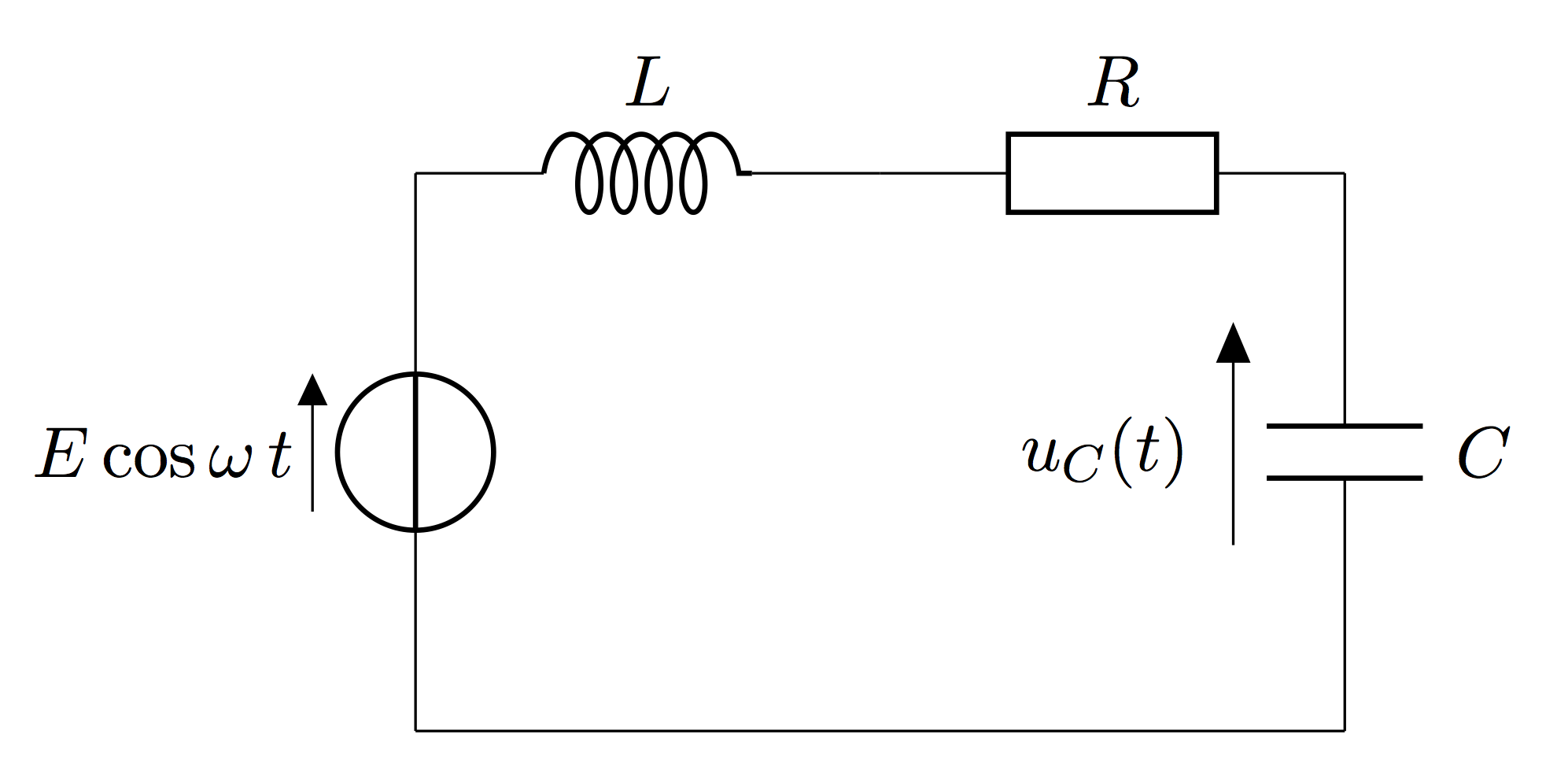
Voilà l’étape qui fait fuir les touristes des mathématiques : appliquer la transformée de Laplace pour dompter une équation différentielle linéaire. Autant vous dire, celui qui saute une ligne ici, il va tout droit au casse-pipe. Prenons un circuit RLC série soumis à un échelon comme fil rouge – rien de mieux qu’un vrai exemple pour éviter le blabla.
Étape 1 : transformer (setup complet)
Soyons concrets. Plaquons la loi des mailles sur le circuit : ( Ri(t) + L\frac{di}{dt} + \frac{1}{C}\int i(t)dt = V_0u(t) )
Maintenant : on pose toutes les conditions initiales (typiquement, i(0) et la tension aux bornes du condensateur), on ne fait pas semblant, c’est la base. Puis,
on balance la transformée de Laplace sur chaque terme. Les dérivées se transforment en multiplications par p, les intégrales en divisions.
$$
R I(p) + L[pI(p)-i(0)] + \frac{1}{C} \cdot \frac{I(p)}{p} = \frac{V_0}{p}
$$
Étape 2 : algèbre dans le domaine p
Là, fini de rigoler. On regroupe tous les I(p) d’un côté et on résout :
$$
I(p)[R + Lp + \frac{1}{Cp}] = \frac{V_0}{p} + Li(0)
$$
On trouve donc directement :
$$
I(p) = \frac{V_0/C}{p(RC+LCp+p^2)} + \text{{membre lié à i(0)}}
$$
Bref, l’équation différentielle se mue en fraction rationnelle dans le monde de Laplace – c’est du calcul de CE2 comparé à l’originale ! (Et là, ceux qui s’obstinent à « simplifier » sans regarder si leur dénominateur est factorisable devraient sérieusement songer à changer de hobby.)
Étape 3 : inversion via Bromwitch ou table
Alors là, deux options. Les puristes tenteront la formule d’inversion intégrale dite de Bromwich :
$$f(t)=\frac{1}{2\pi i}\int_{\sigma-i\infty}^{\sigma+i\infty} F(p)e^{pt}dp$$
Mais soyons clairs : dans la vraie vie, personne ne s’inflige cette boucherie pour un circuit RLC — sauf si vous aimez souffrir ou briller dans les amphis vides du samedi soir.
La tactique ? Décomposer I(p) en éléments simples, piocher dans votre table (sinon Google Images), puis recracher le résultat.
- Pour les impatients : Table express des transformées de Laplace, c’est plus efficace que n’importe quelle formule magique.
- Besoin d’une démo visuelle ? Jetez un œil ci-dessous :
Résoudre une équation différentielle linéaire avec Laplace, c’est troquer une jungle impénétrable contre une autoroute balisée — pour peu qu’on laisse l’automatisme faire le sale boulot.
Applications terrain : où la transformée de Laplace fait le show
Autant vous dire, ceux qui pensent que la transformée de Laplace ne sort jamais du manuel n’ont pas mis les mains dans le cambouis. Dans l’industrie et le labo, elle atomise les équations à la racine — et ce, dans des domaines où personne n’a envie de s’amuser avec les solutions approximatives.
Électricité & électronique : du filtre RC au convertisseur Buck
Trois cas où Laplace rigole des transitoires et stabilise la boutique :
- Filtre RC : La fonction de transfert $H(p)=1/(RCp+1)$ résume tout : réponse aux échelons (transitoire), gain en régime établi (stabilité), le tout analysé d’un trait dans le domaine p — aucun circuit audio sérieux n’échappe à cette moulinette.
- Pont en H (commande moteur) : On modélise l’ensemble pont-moteur avec Laplace pour garantir absence d’oscillations parasites lors des commutations. La stabilité se lit sur les pôles, pas sur une boule de cristal.
- Convertisseur Buck : Grâce à la transformation des équations du filtre d’entrée EMI ou du LC de puissance (Source : ADImodeling), la réponse dynamique et l’atténuation des perturbations sont calibrées à coups de pôles/zéros — zéro place au hasard.
Vibrations mécaniques : amortisseur voiture, pont suspendu
Le système masse-ressort-amortisseur $m\ddot{y}+c\dot{y}+ky=F(t)$ est LE terrain de jeu parfait. Un passage en Laplace ($Y(p)=(F(p)+my_0p+cy_0)/[mp^2+cp+k]$) permet d’isoler modes propres, résonances, amortissement…
Avant j’appelais ça du vaudou ; maintenant je colle direct les conditions initiales dans Y(p), j’identifie pôles/racines et je sais si mon pont vibre comme un spaghetti ou s’il tient debout après un coup de vent. Anecdote vécue : un collègue a « sauvé » une passerelle piétonne uniquement grâce au placement astucieux des zéros/pôles via Laplace. Lui au moins n’a pas appris ça sur TikTok !
Automatique : conception d’un PID comme si de rien n’était
Soyons lucides : synthétiser un PID sans passer par le domaine de Laplace relève du sketch comique. Le contrôleur $C(p)=K_p+K_i/p+K_d p$ s’ajuste finement selon la dynamique voulue, puis on simule la boucle fermée (souvent sous Matlab ou Python). Et pour attaquer le discret ? On traduit $p$ en $z$ via la transformée inverse Z — passage express entre temps continu et numérique garanti maison.
Probabilités : générer une fonction caractéristique en douce
Dans le cirque statistique, la transformée de Laplace devient génératrice des moments. Pour une loi exponentielle ($X\sim \mathcal{E}(\lambda)$), $L_X(t) = E[e^{tX}] = \frac{\lambda}{\lambda-t}$ pour $t<\lambda$. Résultat ? Les moments tombent sans effort, identification de queue (épaisse/fine) incluse. Oubliez les tables lourdingues — c’est plié en deux lignes.
Informatique & signal : déboguer un algorithme de contrôle numérique
Ici on touche au sublime technique. La modélisation symbolique par Laplace sert à anticiper bugs et instabilités avant même d’implémenter l’algo. Les méthodes numériques d’inversion (Talbot, Zakian…) croisent analyse fonctionnelle et calcul symbolique pour vérifier que votre code ne partira pas en oscillation non prévue lors du déploiement réel — bien plus fiable qu’un simple run-and-pray sous Simulink !
Si vous pensiez que la transformée de Laplace restait sur l’étagère du prof grincheux... il est temps sérieusement d’upgrader votre boîte à outils.
FAQ express : les 7 questions qui reviennent toujours
Même en 2024, certains blocages ont la peau dure. Voici l’antidote aux obsessions qui empoisonnent les forums (et les salles de TD) : réponses nettes, pas de redites ni d’enfumage.
Quelle différence avec la transformée de Fourier ?
- Domaine : Laplace bosse sur le plan complexe (p), Fourier se limite à l’axe imaginaire pur (jω).
- Signal : Laplace accepte aussi bien causal que divergents exponentiels ; Fourier exige du stationnaire gentillet.
- Application : Laplace = analyse système/transitoire ; Fourier = spectre pur. C’est pas le même métier.
Puis-je l’utiliser sur une fonction non causale ?
Oui, mais il faut sortir du mode « unilatéral » et passer à la version bilatérale : intégration sur tout R, pas seulement t≥0. C’est utile pour signaux anti-causaux ou pour ceux qui veulent gratter tous les points au concours — dans la vraie vie, 99% des usages restent causaux.
Comment gérer les distributions type Dirac ?
La distribution de Dirac δ(t) n’est même plus un ovni : c’est une fonction généralisée intégrée dans la table officielle des Laplace. Sa transformée vaut 1 pour tout p. Pour traiter ces cas, on applique simplement l’intégration généralisée (sens des distributions) ; ultra-standard en automatique moderne.
Pourquoi une variable complexe p dans Laplace ?
Parce qu’on n’a pas inventé mieux pour capter à la fois croissance, décroissance ET oscillations. La partie réelle contrôle l’amortissement/explosion, l’imaginaire l’oscillation – un deux-en-un chirurgical.
L’inversion de Bromwich, c’est faisable vraiment ?
Théoriquement oui, pratiquement jamais sauf si vous rêvez d’intégrales de contour à l’infini. En pratique : décomposition en éléments simples + table usuelle + Google = boulot fait à 99% !
Comment reconnaître l’abscisse de convergence rapidement ?
Majorez votre f(t) par $Me^{at}$ et choppez a : $\sigma_0 = a$ est LE seuil. Si p reste au-dessus, tout baigne ; sinon, attendez-vous à des sueurs froides.
Les outils incontournables pour ne jamais bloquer ?
SymPy et Wolfram Alpha pour jouer au magicien symbolique ; Matlab/Octave pour manipuler gros systèmes ; Table Laplace PDF à garder sous le coude (clic droit direct dans le navigateur).
Je rembobine : ce qu’il faut retenir (et appliquer dès demain)
Synthèse actionnable
- Identifiez le contexte : vérifiez si votre équation ou système est linéaire à coefficients constants et démarrez par l’écriture des conditions initiales, pas d’approximation foireuse !
- Transformez chaque terme avec la Laplace (dérivées, intégrales, entrées), y compris les conditions initiales. Ne sautez rien, la moindre omission vous explose à la figure.
- Résolvez dans le domaine p : manipulez les fractions rationnelles, factorisez si besoin, et traquez les pôles comme un douanier son faux-monnayeur.
- Invervez proprement : décomposez en éléments simples et récupérez la solution temporelle grâce à vos tables persos (ou une calculatrice en ligne — Google ne juge pas).
- Interprétez physiquement : traduisez chaque pôle/partie réelle/imaginaire pour anticiper stabilité, oscillations ou croissance. Si ça diverge, c’est que vous avez raté une étape !
En vrai : la Laplace dans votre projet d’ingé, c’est carrément le couteau suisse qu’on planque dans sa trousse — et seuls les esprits bornés s’en privent !






