Préparez-vous à l’énoncé le plus brutal de la semaine : comprendre la fonction arctan est sans doute l’une des choses les plus utiles que vous puissiez faire pour vos maths. Autant vous dire qu’il n’en fallait pas plus pour nous donner envie de vous en parler. On vous a préparé un cours ultra-complet sur la fonction réciproque de la tangente. Avec : sa définition formelle, ses propriétés, ses applications concrètes — et même comment la calculer sans calculette (oui, vraiment).
Définition ultra-claire de la fonction arctangente (arctan)
Autant vous dire : si tu penses qu’arctan c’est « 1/tan », t’es déjà dans le décor. L’arctangente – ou fonction arctan – est en fait la fonction réciproque de la tangente, et pas sa vulgaire inverse multiplicative. Ce n’est pas un détail de matheux grincheux, c’est l’essence même du concept.
« Confondre arctan avec 1⁄tan, c’est comme appeler un tigre un gros chat » – Germain Drouet
La formule officielle, la seule qui vaille dans ce bas monde : y = arctan(x), ce qui signifie littéralement que tan(y) = x pour tout nombre réel x. Mais attention, la subtilité mortelle : y ne prend pas toutes les valeurs possibles. Non non, on restreint l’intervalle à ]-π⁄2 ; π⁄2[, c’est-à-dire entre -90° et +90°, ouvert aux deux bouts. Cette restriction n’est PAS une coquetterie d’enseignant frustré : c’est précisément ici que tan(y) réalise une bijection parfaite avec ℝ.
Bijection tangente ↔ arctan et restriction du domaine de la tangente
La fonction tangente, sur l’intervalle ]-π⁄2 ; π⁄2[, balaye strictement tous les nombres réels sans se répéter ni dérailler vers l’infini (hors bornes). C’est seulement dans cette fenêtre ultra-précise qu’on peut inverser proprement : toute valeur réelle x correspond à UN ET UN SEUL angle y.
Soyons clairs : sans cette restriction d’intervalle, la tangente est périodique et donc impossible à inverser proprement. Ici on parle de bijection mathématique, pas d’une vague correspondance hasardeuse.
Propriétés essentielles : parité, continuité, monotonie
Soyons clairs : croire que l’arctan se balade sans structure, c’est négliger le cœur de ses propriétés. Petit fact-check radical.
Parité : l’imparité d’arctan affichée sans fioritures
La fonction arctangente est impaire, point final. Preuve express (pas de blabla inutile) : arctan(–x) = –arctan(x). Pour les sceptiques, vérifiez sur la courbe représentative : symétrie parfaite par rapport à l’origine, la signature même d’une imparité authentique (source sérieuse).
La parité, c’est pas une déco : elle garantit que toute valeur négative renvoie le miroir exact de la valeur positive. Indispensable pour la robustesse des modèles oscillants.
Croissance stricte et continuité : pas de saut, jamais
La fonction arctan est strictement croissante sur ℝ. Sa dérivée, 1/(1+x²), est toujours positive – rien ne peut inverser le sens de variation. Quant à la continuité, elle s’impose sans débat : pas de rupture, pas de saut brutal nulle part. Ça signifie quoi dans la vraie vie ? Aucune zone d’ombre où la courbe s’arrête ou fait un bond — tout glisse doucement vers les asymptotes (cf. preuve).
Asymptotes horizontales y = ±π⁄2 : rôle stratégique
À mesure que x file vers ±∞, arctan(x) s’approche tranquillement de ±π⁄2… sans jamais les atteindre. Ces asymptotes horizontales ne sont pas un gadget visuel : elles servent de « garde-fous » dans les systèmes de contrôle automatique et en traitement du signal. Autant vous dire que pour limiter l’overshoot (le dépassement indésirable), utiliser arctan permet d’avoir une sortie plafonnée par conception ! C’est tout sauf anodin (explications techniques ici).
Anecdote piquante : un vieux système radar soviétique utilisait justement l’arctan pour stabiliser sa sortie face aux signaux parasites extrêmes… Résultat : zéro plantage là où d’autres filtraient à côté.
Dérivée et limites de la fonction arctan
Soyons clairs : l’élégance d’arctan tient à sa dérivée, une formule ciselée qui ne laisse aucune place au hasard. La démonstration ? Basique mais implacable :
Dérivée instantanée : 1/(1+x²), zéro cassure
Pour tout x réel, arctan′(x) = 1/(1+x²). Cette formule n’a pas juste l’air simple, elle EST irréductible : pas de racine, pas d’aberration, aucun point où ça explose (preuve reconnue). Résultat concret : la pente de la courbe ralentit doucement à mesure que x s’éloigne de zéro, mais jamais elle ne s’arrête ou ne « casse ».
Courbe toujours douce, toujours fluide : c’est l’antithèse du signal carré brutal. L’arctan glisse comme un pro sans soubresaut.
Limites aux extrêmes : ça plafonne sec !
Faut arrêter de croire que tout tend vers l’infini… Ici,
- Quand x ➝ +∞, arctan(x) s’approche gentiment de π⁄2.
- Quand x ➝ –∞, arctan(x) titille –π⁄2.
Mais il n’y mettra JAMAIS les pieds. On appelle ça des asymptotes horizontales (cf. preuve), et dans la vraie vie, ça veut dire que la sortie reste bornée — impossible de dépasser le plafond !
Convexité locale : changement pile au centre
Le second effet KissCool mathématique ? Le deuxième dérivé soûle personne, pourtant il y a un twist : pour x<0, la courbe est concave vers le bas, pour x>0 c’est concave vers le haut (source). Moralité : un seul point d’inflexion : pile à zéro. Ce micro-changement influe sur la régularité des modèles prédictifs et explique pourquoi arctan assure une transition subtile entre zone négative et positive.
Représentation graphique : lire l’arctan d’un seul coup d’œil
Construction par réflexion : étapes sans pitié
- Tracer la tangente restreinte : commence par dessiner la courbe y = tan(x), mais seulement sur l’intervalle ]–π⁄2 ; π⁄2[. Hors de cette fenêtre, c’est carnage (asymptotes verticales à ±π⁄2).
- Réfléchir selon y = x : intervertis axes et courbe – l’effet miroir donne le graphe de arctan(x). C’est LE passage obligé pour toute réciproque.
- Vérifier le passage par l’origine : la courbe doit passer par (0,0), stricte obligation mathématique.
- Placer les asymptotes horizontales : y = ±π⁄2. La fonction s’en approche… sans jamais les toucher !
Zones lentes et rapides : lecture critique
La pente de arctan(x) à zéro ? Maximale ! Ici, la variation est ultra-rapide : chaque petit incrément en x fait bondir y. À mesure que |x| grandit, la pente s’écroule quasiment à zéro : la courbe stagne, presque horizontale – évolution ultra-lente aux extrémités. Bref : cœur du graphe = turbo, bords = escargot léthargique.
Vue plan complexe et problème des branches
Dans le plan complexe ℂ, arctan(z) n’est plus aussi docile : il existe des branch cuts, interruptions forcées pour garantir unicité (cf. Wolfram). Pour arctan(z), ces coupures tranchent dans le gras du plan complexe afin d’empêcher des valeurs multiples incohérentes – on ne garde qu’UNE branche principale.
"Arctan n’a rien d’une simple inversion : sa géométrie fait surgir des subtilités insoupçonnées dès qu’on plonge dans le complexe ou qu’on lit sa vitesse de variation."
Comment calculer arctan sans la touche « tan⁻¹ »
Soyons clairs : tabasser la touche « tan⁻¹ » sur ta machine, c’est bien pour les contrôles de collège. Si tu veux comprendre ce qui se trame derrière, c’est tout un monde qui s’ouvre – et franchement, ce n’est pas pour les touristes mathématiques.
Série de Taylor autour de 0 : la méthode à l’ancienne
Voici le développement ultra-canonique (Gregory’s series) :
$$
\arctan(x) = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + ... = \sum_{k=0}^{+\infty} (-1)^k \frac{x^{2k+1}}{2k+1}
$$
Mais attention : cette série ne converge que pour |x| ≤ 1. Plus |x| s’approche de 1, plus il faut de termes pour que l’approximation soit correcte. Pour x = 1 (donc arctan(1) = π/4), il faut des centaines de termes si tu veux trois pauvres décimales fiables. C’est la preuve que savoir manipuler une série, ça ne veut PAS dire qu’on a gagné du temps !
Algorithme CORDIC : quand le CPU lâche les multiplicateurs
En vrai, ta calculette ou ton microprocesseur n’utilise pas du tout la série de Taylor, trop lourde. Il dégaine CORDIC : une méthode itérative qui remplace multiplications et divisions par des additions, soustractions et décalages binaires. À chaque étape, on pivote virtuellement le vecteur par un angle prédéfini (valeur tabulée), on accumule les résultats, et en moins d’une dizaine d’itérations on obtient l’arctan recherché. Simple et brutalement efficace.
Anecdote piquante : Leibniz et son obsession pour π/4
Dans la vraie vie, les ordinateurs du XIXe siècle… étaient des moines scribouillards ! La formule de Leibniz :
$$
\frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + ...
$$
est juste la série de Taylor d’arctan(1). L’ironie ? Cette formule est célèbre mais totalement inefficace en pratique : il faut des millions de termes pour calculer quelques décimales de π. Même les geeks du calcul distribué l’ont vite laissée tomber au profit de variantes plus rapides – petite humiliation historique pour une équation soi-disant mythique.
Applications concrètes de l’arctan dans la vraie vie
Autant vous dire, si tu crois qu’arctan roupille dans un coin de manuel, prépare-toi à pleurer. Son empreinte se retrouve partout où la techno exige des calculs d’angle précis – et pas juste pour épater le prof.
Triangulation GPS : positionnement centimétrique sur Terre
Tu localises ton smartphone à Paris ? Ce n’est pas de la magie noire, c’est du calcul d’angles via arctan entre signaux satellites ! Les stations GPS mesurent la différence de distance avec plusieurs satellites ; chaque différence donne un triangle virtuel. Pour obtenir ta latitude (ou longitude), l’algorithme convertit ces décalages en angle grâce… à l’arctangente, tout simplement :
- On calcule le rapport des variations d’altitude/distance horizontale,
- Et y = arctan(Δh/Δd) te balance directement l’angle sous lequel t’es vu par le satellite (voir StackOverflow pour ceux qui veulent pleurer sur les formules complètes).
Résultat : une précision délirante, jusqu’au centimètre quand les conditions sont optimales. Les géomètres et drones agricoles ne jurent que par ça – et toi tu pinailles encore sur ton DM ?
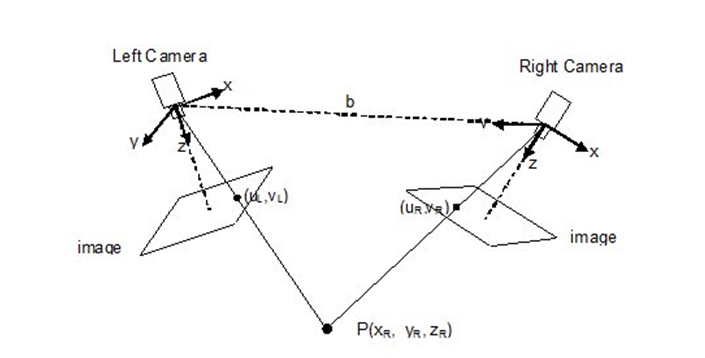
Vision par ordinateur : profondeur 3D instantanée
Arrêtez tout, l’imagerie 3D sans arctan ? Impossible. Dans une caméra stéréoscopique (genre module Intel RealSense ou n’importe quelle vision robotique sérieuse), on capture la même scène sous deux angles distincts. On mesure le « disparity », soit l’écart horizontal entre les deux images d’un même point. Pour convertir ce décalage en profondeur réelle (distance Z), on applique direct :
Z = f * B / arctan(Δx / f)
Où f est la focale et B la base des caméras – sans ce calcul d’arctangente, impossible de modéliser le monde réel en données exploitables pour IA, robots industriels ou jeux vidéo nouvelle génération.
Imagerie médicale, voitures autonomes, drones cartographes… tout ce beau monde carbure à l’arctan caché sous le capot.
Ingénierie du son : phase & filtres audio (IIR/FIR)
Et là, on tape dans le dur de la musique numérique – conception de filtres. La phase d’un filtre audio s’exprime par… arctan(ωRC) ou variantes plus retorses selon le type (IIR/FIR/all-pass). La fameuse « phase response » qui garantit que ton égaliseur ne massacre pas la stéréo ni ne décale les percussions ? C’est encore cette fonction qui fixe mathématiquement le retard entre entrée/sortie sur chaque fréquence. Les ingénieurs mixeurs pro n’utilisent rien d’autre pour ajuster les transitions douces et éviter les artefacts moches dans tes écouteurs.
Récap express : ce qu’il faut retenir pour dompter arctan
Voici la checklist des points à ne PAS zapper si tu veux piloter la fonction arctan comme un boss – et, soyons clairs, rares sont ceux qui cocheraient tout ça sans faillir :
- [x] Définition : Arctan, c’est la fonction réciproque de tan sur l’intervalle ]–π⁄2 ; π⁄2[. Pas une simple inversion naïve.
- [x] Domaine : Elle prend tous les réels en entrée, mais ne crache que des angles dans ]–π⁄2 ; π⁄2[ (soit entre –90° et +90°, ouvert).
- [x] Dérivée : Toujours douce et jamais cassante, c’est 1/(1+x²), donc croissance continue, jamais de rupture.
- [x] Calcul pratique : Série de Taylor pour les puristes, CORDIC pour le hardware. Oubliez le « tan⁻¹ » sur calculette si vous voulez piger ce qui se passe vraiment.
- [x] Applications : GPS, vision 3D, traitement audio… Impossible d’y couper dès que tu veux manipuler des angles en techno réelle.