Découvrez comment élever une matrice à la puissance n efficacement. Ce guide complet vous offre des rappels, démonstrations, méthodes adaptées, cas particuliers et exercices corrigés. Un outil incontournable en algèbre linéaire, souvent redouté pour sa complexité, mais maîtrisable avec les bonnes techniques.
Ce guide a été conçu pour vous permettre de calculer A^n efficacement, en choisissant la méthode adaptée aux caractéristiques de votre matrice.
Au programme :
- Rappels sur la puissance d’une matrice (notation, cas particuliers).
- Trois méthodes adaptées selon le type de matrice.
- Cas particuliers et techniques pour matrices non diagonalisables.
- Démonstrations (récurrence, polynôme annulateur, Binôme de Newton).
- Codes et librairies Python pour simplifier les calculs.
- Exercices corrigés avec solutions détaillées.
- Erreurs courantes à éviter.
- Applications concrètes.
Une pépite de 1500 mots, pensée pour vous faire gagner du temps, des points et des neurones.
Calcul express : la méthode la plus rapide pour élever une matrice à la puissance n
Calculer les puissances de matrices sans méthode peut rapidement devenir source d’erreurs et de confusion. Avant de commencer à calculer A² ou Aⁿ, posez-vous ces trois questions essentielles :
- Quel est l’ordre de ma matrice ? Une matrice doit être carrée pour pouvoir être élevée à une puissance. Si ce n’est pas le cas, le calcul est impossible.
- Ai-je besoin de calculer l’inverse d’A ? Si l’inverse de la matrice est nécessaire (par exemple pour la diagonalisation), il est crucial de vérifier son existence dès le départ.
- Quel type de résultat est attendu ? Résultat symbolique, exact (type λ₁ⁿ) ou numérique ? Le choix de la méthode dépend de l’objectif.
Checklist avant de sortir le clavier
- Ordre : Matrice A carrée obligatoire
- Inversibilité potentielle à tester (et vite)
- Nature du résultat attendu (symbolique / numérique)
Formule éclair : A = P D P⁻¹ ⇒ Aⁿ = P Dⁿ P⁻¹ (et comment Dⁿ se compte en deux lignes)
La diagonalisation est une méthode particulièrement efficace et élégante. Si A est diagonalisable, on a ce Graal matriciel :
A = P D P⁻¹, donc Aⁿ = P Dⁿ P⁻¹. Et là… Pas besoin d’être médaillé Fields pour comprendre que D étant une matrice diagonale, élever D à la puissance n revient juste à élever chaque élément diagonal à la puissance n !
Voici le tableau qui résume ce passage éclair :
| Diagonale initiale D | d₁ | d₂ | ... | dₖ |
|---|---|---|---|---|
| Diagonale de Dⁿ | d₁ⁿ | d₂ⁿ | ... | dₖⁿ |
C’est plié : deux lignes, zéro excuse.
Quand la diagonalisation plante : alternative immédiate via trigonalisation
Certaines matrices ne sont pas diagonalisables, ce qui nécessite des approches alternatives. On ne va pas s’étaler avec des larmes mathématiques : on bascule illico sur la trigonalisation ou les blocs de Jordan. En clair : même non diagonalisable sur R (ou C), toute matrice carrée finit par se réduire en une forme triangulaire supérieure dans une base adaptée — alias « bloc J » si vous causez Jordan.
« Toute matrice peut être analysée avec les bonnes méthodes, même les non diagonalisables. »
Ici le calcul reste possible, moins sexy mais tout aussi implacable : on élève chaque bloc triangulaire puis on retransforme comme un chef grilladin du linéaire.
Puissance d’une matrice : définition opérationnelle et rappels essentiels
Élever une matrice à la puissance n revient à effectuer un produit répété. On prend une matrice carrée A (oui, toujours carrée, sinon c’est la fin des haricots) et on la multiplie par elle-même autant de fois qu’indiqué par l’exposant n. Ni plus, ni moins. Si A n’est pas carrée, partez faire des sudoku.
Ainsi, A² = A × A ; A³ = A × A × A, et ainsi de suite, jusqu’à atteindre l’exposant souhaité. Aⁿ veut simplement dire « je multiplie n matrices identiques entre elles » – point à la ligne.
Notation, conventions et pièges sur les indices
Rendez-vous compte : même dans les bouquins sérieux, on varie entre les notations Aⁿ et A^{(n)} – attention à ce détail qui peut cacher des subtilités lors de lectures croisées ou d’examens corrigés par un prof tatillon.
Points de vigilance sur la notation, indices et parenthèses:
- Toujours écrire l’exposant en haut à droite (jamais en bas !)
- Parenthèses obligatoires si plusieurs matrices ou produits sont impliqués : (AB)² ≠ A²B² sauf cas ultra-spécial !
- Les indices internes (a_{ij}) n’ont rien à voir avec les puissances. Ne mélangez pas tout comme dans le cas fameux de la « matrice Attila » qui, mal notée dans un poly de licence à Paris VI en 1994, a fait rater deux promotions entières.
- La puissance s’applique à toute la matrice — jamais à un coefficient individuel (sauf Hadamard… mais là c’est l’échec assuré).
Cas n = 0 et puissances négatives : pourquoi A⁰ = Iₙ et quand A⁻¹ existe
Attention à ne pas confondre puissance zéro et annulation pure. Par convention stricte : toute matrice carrée élevée à la puissance zéro donne l’identité Iₙ correspondante :
Pour toute matrice carrée A d’ordre n,
[A^0 = I_n]
Pour les puissances négatives (type (A^{-1})), oubliez si votre matrice n’est pas inversible — ce qui arrive bien plus souvent qu’on ne l’imagine !!
L’affaire du binôme de Newton appliqué aux puissances matricielles se traite plus loin — ici on pose juste les bases pour éviter les pataquès.
Trois scénarios MECE pour calculer Aⁿ sans y laisser vos soirées
L’objectif est d’éviter les calculs itératifs longs et inefficaces. On veut du distingué, du chirurgical, trois scénarios mutuellement exclusifs et collectivement exhaustifs (MECE pour les intimes) qui couvrent l’intégralité des matrices carrées. Oui, même celles qui font suer jusqu’aux doctorants.
Scénario 1 : matrice diagonalisable – diagonalisation classique
Si la matrice A est diagonalisable, c’est jackpot :
- On écrit $A = PDP^{-1}$ avec P inversible et D diagonale.
- Les entrées de D sont les valeurs propres de A (attention : la multiplicité algébrique doit coïncider avec la multiplicité géométrique pour chaque valeur propre, sinon c’est l’impasse !).
- La puissance se calcule comme $A^n = P D^n P^{-1}$. Et $D^n$, c’est juste chaque entrée diagonale à la puissance n. Pas besoin de forcer : tout se passe sur la diagonale.
Voici le résumé qui tue :
| Étape | Avantage | Complexité calcul |
|---|---|---|
| Trouver P et D | Vision claire des structures | Peut être pénible selon la taille |
| Calculer $D^n$ | Ultra-direct | Instantané |
| Recomposer $A^n$ | Résultat symbolique ou numérique | O(n³) pour inversion et produits |
Exemple d’entités impliquées : $P$, $D$ (matrice diagonale), $P^{-1}$, multiplicité algébrique vs géométrique.
Scénario 2 : matrice triangulaire – lecture directe
Les matrices triangulaires (supérieures ou inférieures) permettent des calculs rapides et efficaces. \ Pour une matrice triangulaire supérieure stricte ou inférieure stricte, vous montez en puissance en lisant simplement… la diagonale ! Si votre matrice T = (t_{ij}) est triangulaire supérieure :
- $(T^n){ii} = (t{ii})^n$ pour tous i,
- Les coefficients hors-diagonale s’obtiennent par récurrence mais restent prévisibles (on ne détaille pas ici : c’est une gymnastique plus technique mais ça existe).
- Pour une diagonale nulle (strictement triangulaire), toute puissance assez grande donne… zéro partout.
En bref : un œil sur les entrées principales et vous savez tout. Les coefficients non-diagonaux ? Vous pouvez parfois les oublier…
Scénario 3 : matrice nilpotente ou bloc de Jordan – stratégie mixte (N + D)
Alors là, on sort le grand jeu. Quand A refuse obstinément toute diagonalisation, mais qu’elle n’est pas non plus gentille et triangulaire dans son coin… on attaque par blocs de Jordan ou via une décomposition $A = D + N$ où D est diagonalisable (souvent scalaire multiple d’identité dans ce cas), N nilpotente ($N^k=0$ à partir d’un certain k). \ Cette situation arrive plus souvent qu’on ne croit : une matrice nilpotente d’ordre k donne automatiquement $A^k = 0$. Pour un bloc de Jordan associé à une valeur propre λ :
- La formule générale exploite le binôme de Newton matriciel : $(D+N)^p = \sum_{j=0}^p \binom{p}{j} D^{p-j} N^j$.
- Le calcul reste faisable car tous les termes avec $N^j$ pour j grand s’annulent rapidement !
Toute matrice finit par révéler son jeu si on la cuisine assez longtemps — même les non diagonalisables.
Vous voilà armé pour affronter même les copies piégées par vos profs favoris.
Plan B : techniques universelles quand votre prof ou votre logiciel dit « non diagonalisable »
Soyons clairs : quand la matrice joue les rebelles et refuse la diagonalisation, c’est le moment de sortir l’artillerie lourde. Inutile de pleurnicher devant le terminal Python ou d’errer sur StackOverflow : il existe trois méthodes qui marchent, même pour les cas désespérés.
Démonstration par récurrence et conjecture supervisée
Dans le monde académique, la preuve par récurrence se déroule comme un ballet bien huilé :
- Initialisation : Vérifiez le résultat pour n = 1 (souvent trivial).
- Hypothèse de récurrence : Supposons que la formule marche pour n = k.
- Hérédité : Montrez qu’elle tient pour n = k+1 en utilisant la multiplication matricielle et l’hypothèse précédente.
- Clôture : Terminez en disant « donc vrai pour tout n ≥ 1 » – standing ovation.
Dans la vraie vie ? Vous commencez toujours par conjecturer $A^n$ à partir des premiers calculs (Python peut aider). Si le motif est là, on emballe vite la récurrence. Soyons honnêtes : personne ne fait durer ça plus de dix minutes.
Étapes typiques (ne jamais zapper) :
- Calculer plusieurs puissances ($A$, $A^2$, $A^3$)
- Chercher un motif dans les coefficients
- Conjecturer une formule générale
- Récurrence pour valider
Polynôme annulateur et théorème de Cayley-Hamilton
Autant vous dire : si A est non diagonalisable, Cayley-Hamilton devient votre partenaire officiel. Toute matrice carrée annule son polynôme caractéristique $p_A(X)$, c’est-à-dire que $p_A(A) = 0$. Résultat ? On peut toujours exprimer $A^n$ comme une combinaison linéaire des puissances précédentes ($I$, $A$, $A^2$, ..., $A^{d-1}$ où d = degré du polynôme). En pratique :
- Trouvez le polynôme caractéristique de A (à la main ou à l’arrache avec Python).
- Exprimez $A^d$ en fonction des puissances inférieures : par exemple, si $A^3 - 4A^2 + 5A - 2I = 0$, alors $A^3 = 4A^2 - 5A + 2I$. Ainsi, toute puissance supérieure peut se ramener aux précédentes.
- Pour obtenir $A^n$, déroulez la relation — c’est bourrin mais ça donne une expression fermée, même pour des matrices avec historique judiciaire !
Binôme de Newton appliqué aux matrices sommables (D + N)
Quand A s’écrit comme somme d’une diagonale D et d’une nilpotente N qui commute avec D ($DN=ND$), alors on sort direct le binôme newtonien matriciel :
$$
(D+N)^n = \sum_{k=0}^n \binom{n}{k} D^{n-k} N^k.
$$
Cas d’école ? N nilpotente ($N^{m}=0$ dès que m atteint l’ordre), donc seuls quelques termes survivent dans la somme ! Autant vous dire que c’est du pain béni pour calculer rapidement de hautes puissances sans s’arracher les cheveux sur chaque bloc Jordan.
« Les démonstrations by-the-book sont parfaites… pour louper son train : on veut du concret qui tourne sur Python. »
Algorithmes et outils numériques pour la puissance rapide d’une matrice
Utiliser une méthode inefficace comme le produit manuel répété est une perte de temps considérable. L’exponentiation binaire écrase tout sur son passage : au lieu de se farcir n multiplications (méthode classique), ici le boulot tombe à O(log n). Oui, logarithmique, pas linéaire : le genre de truc qui fait pleurer les profs d’analyse.
Exponentiation binaire : O(log n) multiplications, pas une de plus
L’algo est simple comme « bonjour », à condition d’avoir dormi pendant le cours de bits…
Pseudo-code express pour Aⁿ (A matrice carrée, n entier ≥ 0) :
1. Résultat ← Identité
2. Tant que n > 0 :
- Si n impair : Résultat ← Résultat × A
- A ← A × A (carré)
- n ← n // 2 (division entière)
3. Retourner Résultat
Utilisez cet algo pour calculer un bloc de Jordan J^n sans tomber dans la folie itérative.
| Étape clé | Multiplications cumulées (classique) | Multiplications cumulées (binaire) |
|-----------------------------|--------------------------------------|------------------------------------|
| Puissance n = 10 | 9 | 4 |
| Puissance n = 100 | 99 | 7 |
| Général (ordre de grandeur) | O(n) | O(log₂(n)) |
L’exponentiation binaire vous sauve littéralement la mise dès que n dépasse une dizaine. Les réfractaires peuvent toujours coder des boucles for… et perdre leur week-end.
Tour d’horizon des librairies Python/Julia/R qui font le boulot
Si vous effectuez encore vos produits matriciels manuellement, il est temps de passer à des outils numériques. Les pros utilisent ces outils :
- Python : numpy.linalg.matrix_power(A, n) — Version requise : NumPy ≥1.6.
- Julia : LinearAlgebra fournit l’opérateur A^n natif dès Julia v1.0.
- R : package expm (expm::%^% ou expm::MatrixPower) — indispensable dès qu’on dépasse les matrices jouets.
Au niveau perf : NumPy utilise l’exponentiation rapide (logarithmique), Julia va aussi vite mais syntaxe encore plus clean, R rame un peu sur les gros blocs mais tient la barre jusqu’à quelques centaines d’ordres sans crash majeur.
> Les démonstrations by-the-book sont parfaites… pour louper son train : on veut du concret qui tourne sur Python.
Mode d’emploi de la calculatrice en ligne dCode (et limites pratiques)
dCode.fr propose un outil net et sans bavure pour élever une matrice à une puissance quelconque :
- Saisir votre matrice dans les cases prévues (dCode puissance matrice).
- Indiquer l’exposant désiré.
- Cliquer, patienter trois secondes : résultat immédiat, avec détails si demandé.
dCode digère tout type de matrices carrées jusqu’à l’ordre 10–12 (au-delà c’est aléatoire suivant votre PC), gère entiers/rationnels/flottants, mais oubliez-le pour les matrices géantes (>15×15) ou pour les calculs exacts sur très grands entiers — là-dessus, rien ne vaut un vrai script maison.
Exercices corrigés : passez du théorique au concret
Les puissances de matrices prennent tout leur sens avec des exercices concrets. Voici trois cas réels qui, eux, valent leur pesant d’algèbre.
Exercice 1 : A diagonalisable 2×2 – résultat en trois lignes
Énoncé
Soit $A = \begin{pmatrix}3 & 1\0 & 2\end{pmatrix}$.
Calculer $A^n$ pour tout entier $n \geq 1$.
Correction (step by step)
1. Détermination des valeurs propres : $\det(A-\lambda I) = (3-\lambda)(2-\lambda)$. Les valeurs propres sont donc $3$ et $2$.
2. Vecteurs propres associés : Pour $\lambda=3$, vecteur propre $(1,0)^T$. Pour $\lambda=2$, vecteur propre $(1,-1)^T$.
3. Matrice de passage P et diagonale D :
- $P = \begin{pmatrix}1 & 1\0 & -1\end{pmatrix}$ ; $D = \begin{pmatrix}3 & 0 \0 & 2\end{pmatrix}$
4. Puissance n-ième : $A^n = P D^n P^{-1}$.
5. Calcul explicite
$$A^n = \begin{pmatrix}3^n & (3^n-2^n) \0 & 2^n\end{pmatrix}$$
Moralité : diagonalisable ? Résultat lisible en deux minutes top chrono !
Exercice 2 : matrice nilpotente 3×3 – trouver l’ordre de nilpotence
Énoncé
Soit $N = \begin{pmatrix}0 & 1 & 0 \0 & 0 & 1 \0 & 0 & 0\end{pmatrix}$.
a) Déterminer l’ordre de nilpotence de N.
b) Calculer $N^k$ pour tout entier $k \geq 1$.
Correction détaillée
a) Calculons les puissances successives :
- $N^1 = N$
- $N^2 = \begin{pmatrix}0&0&1\0&0&0\0&0&0\end{pmatrix}$
- $N^3 = O_3$
Donc, ordre de nilpotence : k=3, car $N^3=O_3$ et pas avant !
b) Par définition : pour tout k ≥ 3, N^k=O_3 ; pour k=1 ou k=2, calculez explicitement comme ci-dessus.
Checklist — Identifier le degré de nilpotence
- Calculer N¹, N²… jusqu’à obtenir la matrice nulle Oₙ
- Vérifier que tous les coefficients s’annulent au rang minimal obtenu
- Contrôler s’il existe une combinaison linéaire ramène la matrice à zéro plus tôt (spoiler : pas ici)
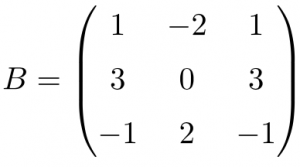
> Les matrices nilpotentes ne mentent jamais : toute puissance supérieure à l’ordre donne zéro — c’est implacable !
Exercice 3 : matrice triangulaire non diagonalisable – lecture + récurrence
Énoncé
Soit $T = \begin{pmatrix}4 & 1 & 0 \0 & 4 & 1 \0 & 0 & 4\end{pmatrix}$.
Calculer $T^p$ pour tout p ∈ ℕ*, donner le schéma général.
Correction bien frappée :
a) T est triangulaire supérieure avec tous ses coefficients diagonaux égaux ($4$), mais elle refuse catégoriquement la diagonalisation, faute d’autovecteurs distincts (multiplicité géométrique < multiplicité algébrique).
b) On lit directement sur la diagonale :
pour tout i, $(T^{p}){ii}=4^{p}$ (ça, c’est cadeau).
c) Hors-diagonale : par récurrence,
pour les coefficients $(i,j)$ ($j>i$), on obtient : $(T^{p}){i,j}=C_{j-i}(p)4^{p-(j-i)}$, où C dépend du nombre de chemins (laissez tomber les détails si vous ne voulez pas y passer votre nuit).
d) Tout ce qui est au-dessus du premier hors-diagonale gonfle selon des polynômes en p, mais attention aux erreurs classiques : ne surtout pas prendre T comme diagonalisable ni supposer que seuls les éléments diagonaux survivent !
e) Résultat spécifique pour p=3 donné à titre d’exemple (pour vérifier à la main).
Erreurs courantes et pièges à éviter quand on joue avec Aⁿ
Confondre puissance matricielle et produit Hadamard : le faux ami
Chaque année, des armées d’étudiants tombent dans le panneau : ils mélangent puissance classique (Aⁿ) et produit de Hadamard (noté ⨀). Soyons clairs : la puissance matricielle c’est du « produit ligne par colonne répété », alors que le produit de Hadamard c’est juste l’élévation coefficient par coefficient. Rien à voir, aucune compassion si vous mélangez tout.
Prenez A = (\begin{pmatrix}2 & 3\1 & 0\end{pmatrix}) :
- Puissance matricielle A² = A × A = (\begin{pmatrix}7 & 6 \2 & 3\end{pmatrix})
- Puissance Hadamard A^{⨀2} = (\begin{pmatrix}4 & 9\1 & 0\end{pmatrix})
Résultat : seul le premier donne la dynamique linéaire qu’on attend.
Oublier les conditions de diagonalisation : échec assuré
Avant de sortir la formule magique A = PDP⁻¹, il faudra franchir ces checkpoints sans tricher :
- Le polynôme caractéristique doit être scindé sur le corps considéré (toutes les valeurs propres sont là, sans racine manquante).
- Pour chaque valeur propre λ, la dimension du sous-espace propre (=multiplicité géométrique) doit égaler sa multiplicité algébrique. Autant vous dire : s’il manque un seul auto-vecteur, c’est plié !
- Matériellement, il faut n vecteurs propres linéairement indépendants pour une matrice d’ordre n.
- Si une seule de ces conditions part en sucette ? Adieu diagonalisation, bonjour trigonalisation ou Jordan.
Sous-estimer la stabilité numérique : précipice algorithmique garanti
Dans la vraie vie, élever une matrice à un grand n en calcul numérique peut faire exploser l’ordinateur… ou pire, donner des résultats absurdes. Les risques ?
- Débordement : certains coefficients deviennent gigantesques (overflow), tout explose.
- Perte de précision : multiplication répétée ≈ accumulation d’erreurs d’arrondi (surtout sur les valeurs propres proches de zéro ou très grandes).
- Matrice mal conditionnée ? Attendez-vous à voir vos chiffres partir en vrille après quelques puissances.
Pour éviter ce naufrage : privilégiez l’exponentiation binaire (moins d’opérations), surveillez le conditionnement et bossez sur des matrices normalisées dès que possible. Les « erreurs invisibles » font plus de dégâts que tous les profs sadique réunis.
Applications éclair : pourquoi s’embêter avec la puissance d’une matrice ?
Les puissances de matrices ont de nombreuses applications pratiques, bien au-delà des exercices académiques. Trois domaines majeurs exploitent ce concept — et pas juste pour frimer devant un tableau blanc.
Chaînes de Markov : prédire l’état après n pas
Pour une chaîne de Markov à états finis, la matrice de transition $P$ élevée à la puissance $n$ (${P}^n$) donne la probabilité de passer de n’importe quel état initial à n’importe quel état final… en n étapes. Autant vous dire que sans cette puissance, impossible d’estimer l’état du système sur le long terme ou de détecter les comportements stationnaires. (Cf. State Probability Distributions: $P^n$ donne directement la probabilité après $n$ transitions.)
Systèmes dynamiques discrets : croissance, population, trafic
Dans les modèles de population (genre Leslie ou matrices écologiques), on projette l’évolution d’espèces ou du trafic urbain par des multiplications itérées d’une matrice à chaque génération. Vous voulez savoir combien d’individus dans 50 ans ? On élève la matrice démographique à la puissance 50 et on applique au vecteur initial — résultat immédiat, pas besoin de boule de cristal ni de bouton Excel foireux.
Cryptographie et exponentielle de matrices : teaser explosif
Certaines méthodes de chiffrement (cf. chiffrement de Hill ou codes cycliques) reposent sur des puissances matricielles pour embrouiller le message clair. La vraie pépite ? L’exponentielle matricielle ($e^{A}$), utilisée dans certains algos avancés (et oui, même dans certains schémas robustes contre les attaques quantiques). Rapprochez-vous bientôt du mythe « Matrice Attila »… et préparez-vous à voir vos messages secrets passer la vitesse supérieure !
Le calcul matriciel n’est pas réservé aux matheux fous : il fait tourner vos modèles prédictifs, vos simulations écolos et même vos protocoles secrets.
Pour aller plus loin : l’inverse d’une matrice avant l’exponentiation
Soyons clairs : maîtriser l’inverse d’une matrice, c’est la clé pour ne pas se manger un mur à la première puissance négative. Si A n’est pas inversible, oubliez direct tout calcul du type $A^{-n}$ : ça n’a strictement aucun sens mathématiquement (et ça ne tournera jamais en Python). Autant vous dire que les propriétés de puissances négatives sont valides uniquement quand la matrice est inversible — sinon c’est retour à la case départ comme un bleu. Pour vraiment piger les conditions et éviter les embrouilles sur $A^{-1}$, foncez lire le guide dédié Guide complet sur l’inverse d’une matrice.
Ce qu’on retient (et ce qu’on jette) sur la puissance d’une matrice
Dernière cartouche avant de passer à l’action. Autant vous dire que ceux qui retiennent tout, ne digèrent rien. Soyons clairs, il faut faire le tri :
Checklist — Trois idées à graver dans le marbre, une à bazarder :
- 1. Diagonalisation = jackpot. Quand c’est possible, foncez : Aⁿ se calcule en trois opérations mentales sans lâcher votre mug.
- 2. Méfiez-vous des matrices « rebelles ». Nilpotentes ou non diagonalisables ? Blocs de Jordan, récurrence et Cayley-Hamilton sont vos alliés — mais la flemme n’a jamais sorti personne de la panade.
- 3. Exponentiation binaire ou rien. Si vous tapez chaque multiplication à la main, autant tricoter une corde pour votre clavier.
- ❌ À jeter : Confondre puissance matricielle et Hadamard. C’est l’erreur des amateurs et ça ruine tout, sans appel.
Passez au clavier, testez vos propres matrices, plantez-vous vite et fort… mais avec méthode : c’est comme ça qu’on apprend pour de vrai !






